

Research activities in the NA group
Numerical analysis for stochastic and deterministic differential equations with applicationsStochastic and deterministic differential equations are fundamental for the modeling in Science and Engineering. As the computational power increases, it becomes feasible to use more accurate differential equation models and solve more demanding problems: for instance to determine parameters from fundamental principles, to optimally estimate parameters using measurements, or to find the optimal construction of a design.There are therefore two interesting computational sides of differential equations:
MembersHåkon Hoel, PhD studentAshraful Kadir, PhD student Love Lindholm, PhD student Mattias Sandberg, Associate Professor Anders Szepessy , Professor Raul Tempone, Associate Professor Contact someone in the group for more information on master-thesis projects, Ph.D-projects, papers etc. Computational Technology LaboratoryCTL homepageThe mission of the Computational Technology Laboratory is to develop new technology for computation characterized by generality, reliability and efficiency. Interaction with society and industry is an important part of CTL, with collaborative projects to develop new technology with computation. In university education the role of CTL is to promote the new computational technology on all levels. The research at CTL aims at unifying fundamental research on mathematics and computation with advanced applications of industrial interest. The core of CTL research is based on first principle computational mathematical modeling, with differential equations and adaptive finite element methods, and with implementation of the computational technology in the open source project FEniCS. CTL also strives to initiate joint projects with experts from other disciplines. 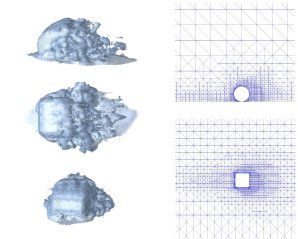
Simulation of turbulent flow, without any turbulence modeling, past a rotating wheel using a finite element method with adaptive mesh refinement
Group LeaderJohan Hoffman, ProfessorMembersNiyazi Cem Degirmenci, PhD studentJohan Hoffman, Professor Johan Jansson, Senior researcher Niclas Jansson, PhD student Aurelien Larcher, PostDoc Kaspar Müller, PhD student Jeannette Hiromi Spühler, PhD student Rodrigo Vilela De Abreu, PhD student For more detailed information, see the CTL homepage . For master thesis projects, job opportunities, etc., contact Johan Hoffman. Computational modelling of the mammalian cellThe objective of our research is to generate realistic and computationally effective models of cellular metabolism. By taking advantage of the versatile properties of enzyme systems that metabolize reactive, hydrophobic compounds we can utilize excellent control over processes that occur intracellularly. The experiments give precise information on localization and enzymatic conversion of probe molecules. A particularly challenging aspect is the modelling of the partition of hydrophobic compounds (important as hormones, signalling molecules and medical drugs). An integrated part of the project involves the generation of efficient, versatile and computationally tractable models of cellular reactions and diffusion (using fundamental/experimentally determined constants) which are verified against experimental data. Contributions towards an accurate computational model of the cell will be of great importance for basic science and drug development.Research leaderMichael Hanke, Associate ProfessorMembersQasim Ali, PhD studentCooperation withRalf Morgenstern, prof., Karolinska InstitutetBengt Jernström, prof., Karolinska Institutet Multi-phase FlowThe area of multi-phase flows is a very rich and active field of research. Our numerical simulations will enhance the understanding of various complex flows, for example the dynamics of fiber suspensions and the effect of surfactants in processes on the micro-scale.We are developing several different numerical methods to simulate these problems. The conservative level-set method has reduced mass conservation errors usually associated with this class of schemes, and is now being extended to handle contact problems such as the wetting of drops on a solid surface. A completely new surface representation for dynamic interfaces separating immiscible fluids is being developed together with algorithms to simulate the evolution of surface active agents. Boundary integral methods together with high performance computing allow for large scale simulations of fiber suspensions. Research on so called fast summation methods is performed to further accelerate these simulations. We are a partner in the Linne Flow Centre at KTH, and enjoy the collaborations within the "Micro and complex fluids" working group, joining researchers performing theoretical, numerical and experimental work within this exciting field. 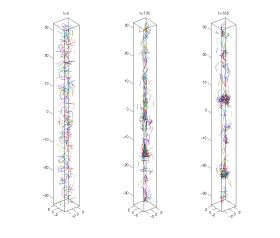
Simulation of sedimenting fibers. Initially the distribution is random and uniform. Clusters of fibers form as time proceeds and fall more quickly than single fibers.
MembersJennifer Grünig, PhD studentKatarina Gustavsson, Assistant Professor Ludvig af Klinteberg, PhD student Rikard Ojala, PostDoc Anna-Karin Tornberg, Associate Professor, group leader Oana Wiklund, PhD student Associated researchersGunilla Kreiss, Professor, Uppsala UniversitySara Zahedi, Uppsala University Computational High Frequency Wave PropagationSimulation of high-frequency waves is a problem encountered in a great many engineering and science fields. Currently the interest is driven by new applications in wireless communication (cell phones, Bluetooth, WiFi) and photonics (optical fibers, filters, switches). Simulation is also used increasingly in more classical applications. Some examples in electromagnetism are antenna design, radar signature computation and base station coverage for cell phones. In acoustics simulations are used for noise reduction, underwater communication and medical ultrasonography. Locating earthquakes and oil exploration are some applications of seismic wave simulation in geophysics.The main numerical difficulty of these problem stems from the fact that the domain of interest is large compared to the wavelength of the solutions; the essential frequency is high. This is a major challenge for traditional numerical simulation methods, since their computational cost increases at least algebraically with the frequency. Realistic problems can become prohibitively expensive already for moderately high frequencies.
MembersJelena Popovic, PhD studentOlof Runborg, Associate Professor, group leader Multiscale MethodsIn this project we study computational methods for problems with multiple scales in time and space. Examples of such problems are abundant and include turbulent flow, structural analysis of composite materials, flow through porous media, weather forecasting, complex fluids, many-body galaxy formation, and large-scale molecular dynamic simulations. The fine scales often have a strong effect on the coarse scale dynamics, and must be taken into account in the numerical scheme. Large differences in scales, temporal and/or spatial, therefore make direct numerical simulations very expensive, since the fine scales need to be resolved over large scales; the number of degrees of freedom in the numerical simulation becomes very high.The objective of this project is to construct numerical methods for simulating multiscale problems, which significantly reduce the complexity compared to direct simulation on the fine scale model, while still maintaining high accuracy. One such class of methods is heterogeneous multiscale methods (HMM). It has emerged as an efficient framework for development and analysis of numerical multiscale methods that couple algorithms for different scales. In HMM, an algorithm is set up to simulate the macroscale directly. Local micro-scale simulations are then used to produce potentially missing data for the macro-scale algorithm. For practical problems, this can often be seen as replacing heuristics and empirical observations in coarse scale single physics models by direct numerical simulations of more accurate models defined on finer scales. HMM thus overcomes the numerical difficulties by only resolving the micro-scale over small domains in time and space. Under certain assumptions, this gives enough information to properly simulate the macroscopic behaviour of the system. 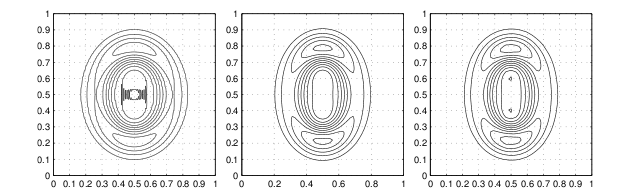
The wave equation with a rapidly varying material parameter in two
dimensions. Comparison between fully resolved solution (left), the
solution to the homogenized problem (middle) and an HMM solution
(right).
MembersDoghonay Arjmand, PhD studentBjörn Engquist, Professor, group leader Olof Runborg, Associate Professor Computational Electromagnetics in Complex EnvironmentsIn the planning and design of antenna systems for wireless communication, simulation of the Maxwell equations can be a valuable complement to in situ measurements. Detailed simulations in complex environments give rapidly varying solutions because of the short wavelength relative the geometry and of the multitude of reflected and diffracted waves. Pointwise accurate solutions therefore require a very detailed modeling of the geometry, electrical properties of materials, source location, frequency and many other parameters that, in practice, are not known or are uncertain. The resulting numerical problem will also involve very many unknowns and large computer resources are necessary to solve it.Pointwise values of the electromagnetic field are, however, often not of great practical importance. Instead, one is interested in simplified descriptions, e.g. "channel models", which only consider local averages, variances and other statistical measures of the field and the power, and how these depend on a smaller number of parameters (distance to source, frequency, type of terrain, etc.). This project concerns the mathematical and numerical problems related to the construction of new improved such models based on direct numerical simulations and analysis. It is a project within the Center of Industrial and Applied Mathematics (CIAM) and is a collaboration with Ericsson Research. MembersBjörn Engquist, Professor, group leaderJon Häggblad, PhD student Olof Runborg, Associate Professor |