Avancerade grafalgoritmer
Det här får nog tas mer som kuriosa än som användbart
för tävlingsuppgifter. Åtminstone har jag inte använt
det själv. Men eftersom det hänger ihop med annat som har tagits
upp tidigare, tyckte jag det kunde vara kul.
1. Bellman-Ford's algoritm för kortaste vägen
Detta är i och för sig ingen avancerad algoritm, tvärtom är det enkelheten som är trevlig, det kan vara bra att veta att en ganska intuitiv lösning verkligen ger kortaste vägen. Algoritmen är så här (w(e) är vikten på bågen e och start är den nod man vill veta kortaste vägen från)
BELLMAN-FORD
dist[v] := INF för varje nod v // INF = t.ex. 1000000000
dist[start] := 0
repeat
changed := FALSE
for varje båge e = (u, v) do
if dist[u] + w(e) <
dist[v] then
dist[v]
:= dist[u] + w(e)
changed
:= TRUE
until not changed
Om man skriver på detta sätt förutsätter man att
grafen inte innehåller några cykler med negativ vikt, då
skulle den ju fortsätta i all evighet. Däremot får bågarnas
vikter vara negativa. Vill man explicit kolla efter negativ-vikt-cykler kan
man använda sig av det faktum att om det inte finns några sådana
så körs repeat-loopen högst V-1 gånger, där
V är antalet noder. Vill man explicit veta den kortaste vägen
kan man precis som i Dijkstra's ha ett "föräldraträd" genom
att när man uppdaterar dist också skriva
parent[v] := u
För att få Bellman-Ford i sitt sammanhang kan man skriva upp
kortaste-väg-algoritmerna i en tabell.
| Algoritm |
Komplexitet |
Klarar negativa vikter |
| Dijkstra's utan heap |
O( V2 ) |
NEJ |
| Dijkstra's med heap |
O( E log V ) |
NEJ |
| Bellman-Ford's |
O( EV ) |
JA |
| Floyd-Warshall's (all pairs shortest paths) |
O( V3 ) |
JA |
Så vilken som är absolut bäst beror lite på hur
tät grafen är. Om E = O(V^2), d.v.s. grafen är nära
komplett, så är det t.ex. bättre att köra Dijkstra's
utan heap än med heap (detsamma gäller förresten
Prim's algoritm för MST, tack Erik). Och Floyd-Warshall's är
då i stort sett lika snabb som Bellman-Ford's, även ifall man
bara behöver en enstaka kortaste väg, så då kan man
ju välja algoritm efter hur man har grafen sparad, eftersom Floyd-Warshall's
kräver matrisform. Om grafen är gles så är ju Bellman-Ford's
bra när man har negativa vikter, och kanske annars också om man
råkar ha grafen sparad som en lista med bågar.
2. Viktad bipartit matchning
Detta är en variation på maximala matchningsproblemet
. Vi har en viktad bipartit graf och vill hitta den matchning
som maximerar summan av de valda bågarnas vikter. Problemet uppkommer
exempelvis om n personer söker n jobb och varje person
har en "lämplighetsfaktor" för varje jobb. Hur ska man fördela
jobben så att den sammanlagda lämpligheten blir så stor
som möjligt? Att testa alla n! kombinationer känns ofta
lite jobbigt, så det är tur att det finns en bättre lösning.
De effektivaste algoritmerna bygger på dual variables som
är en sorts viktstilldelningar för noderna. Om ni är intresserade
kan ni ju läsa
här
(välj "PS.gz" och byt namn på filen till .ps), jag blir inte
klok på det själv. Vill ni in på riktigt svåra grejer
så titta på det
generella fallet
(välj "A paper describing...") då grafen inte är bipartit.
Den algoritm som återges nedan känns enklast tycker jag, och
komplexiteten O(V^4) är för täta grafer inte sämre
än den enklaste dual-algoritmen (Hungarian search). Här förutsätts
n personer och n jobb och en "komplett graf" (så långt
det går i en bipartit graf), d.v.s. varje person söker alla jobb.
WEIGHTED_MATCHING
M := {} //kommer att fyllas på med bågar som ingår i
matchningen
Upprepa n gånger
Bilda en ny komplett riktad graf (2n noder, bågarnas
vikt nw) med
utgångspunkt från den givna
grafen (vikt w) genom att
för varje båge
e = (u, v) sätta
nw(e) := 0 om
u = v
INF om både u och v är personer
INF om både u och v är jobb
INF om e ingår i den aktuella matchningen M
-w(e) om u är en person och v är ett jobb och e inte ingår
i M
w(e) om u är ett jobb och v är en person och e inte
ingår i M
Kör FLOYD-WARSHALL på nya grafen
Sök igenom matrisen och välj den kortaste vägen
från en omatchad person
till ett omatchat jobb. Denna väg
är p.g.a. viktningen ovan en s.k.
augmenting path.
Gå längs den funna vägen och förskjut
matchningsbågarna i M på följande sätt:
Före: a b-c d-e f Efter:
a-b c-d e-f
Detta utökar M med en båge precis som i den
oviktade matchningsalgoritmen
Skillnaden mellan den vanliga matchningsalgoritmen och denna algoritm är alltså att i den förstnämnda kan man välja vilken augmenting path som helst, slutmatchningen blir alltid optimal ändå, men i ovanstående algoritm måste den kortaste vägen (i det avseende som definieras av nw) väljas i varje steg för att garantera att slutmatchningen får maximal vikt. Beviset för att det verkligen blir så har jag faktiskt inte sett, är det någon som kan ge det?
3. Kinesiska brevbärarproblemet
Detta problem beskrevs redan under Hamilton- och Eulerkretsar , men nu har vi verktyget för att lösa det, åtminstone i det fall då grafen är riktad. Det gäller alltså att hitta en rundtur som besöker alla bågar minst en gång men som ändå är så kort som möjligt (med avseende på bågarnas sammanlagda vikter), precis som när man delar ut post i ett villaområde. Vi förutsätter hädanefter att grafen är riktad och att den består av en enda starkt sammanhängande komponent (annars kommer brevbäraren aldrig tillbaka).
Det bästa vore naturligtvis om man kunde hitta en Eulerkrets, eftersom den alltid är optimal. Kriteriet för att det finns en Eulerkrets är enkelt: om varje nod har lika stor utgrad som ingrad så finns det alltid en sådan, och den kan konstrueras på samma cykelkopplingssätt som beskrevs för oriktade grafer i Hamilton- och Eulerkretsar . Annars skulle man vilja lägga till bågar mellan de "jobbiga noder" som inte har ingraden lika stor som utgraden. Men brevbäraren måste naturligtvis fortfarande följa de bågar som finns, så vikten av de nya bågarna blir helt enkelt den kortaste vägen mellan noderna i ursprungsgrafen. Om det finns många jobbiga noder gäller det att bestämma vilka par som ska förbindas för att summan av vikterna ska bli så liten som möjligt, och det är här som viktad bipartit matchning kommer in.
Alltså, rent praktiskt:
1. Låt Z(u) för varje nod u beteckna Ingrad(
u) - Utgrad( u)
2. Använd t.ex. Floyd-Warshall's algoritm för att hitta kortaste
vägarna mellan noderna med Z != 0.
3. Skapa en ny, bipartit, "komplett" graf där varje gammal nod u ger
upphov till |Z| nya noder, vilka hamnar till vänster om Z
>0 och till höger om Z<0. Om t.ex. Z(u) = -3 ger
u upphov till tre noder på högersidan med identiska uppsättningar
bågar. Bågarnas vikt sätts lika med kortaste vägen
från steg 2.
4. Använd algoritmen ovan för att hitta en fullständig matchning
med minimal vikt (byt tecken på nw för att få minimum).
5. Lägg i den ursprungliga grafen till de bågar som ingår
i de kortaste vägar som väljs i matchningen och konstruera en Eulerkrets
i den utökade grafen.
Uppgift 1: Visa att den bipartita grafen har lika många noder
till höger och vänster.
Uppgift 2: Visa att problemet för en oriktad graf ger upphov
till viktad matchning i en generell graf, vilket är mycket svårare.
Uppgift 3: Implementera ovanstående algoritm om du känner
för det.
4. Hopcroft-Karp's algoritm för bipartit matchning
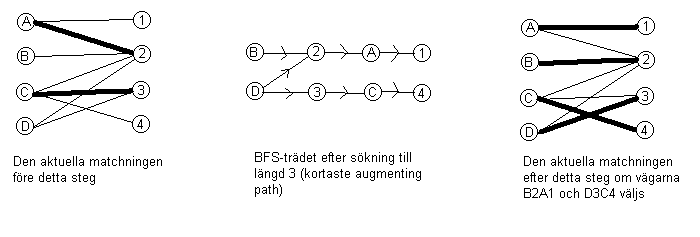
Till sist tänkte jag säga något om den beryktade Hopcroft-Karps matchningsalgoritm, som skulle ha behövts för att få full poäng på Knights (nu kom ju folk inte riktigt så långt, maxpoängen blev bara 40/100 på den uppgiften). Här snackar vi alltså oviktad matchning igen, och det är inget konstigt alls. Istället för att välja bara en augmenting path i taget, hittar man flera stycken på en enda sökning. Om dessa inte har någon nod gemensamt kan man ju sedan göra omflyttningarna i vilken ordning som helst. Så i varje utökningssteg gör man en BFS-sökning där man börjar med att i kön (med avstånd 0) lägga alla omatchade noder på vänstersidan och sedan fortsätta sökningen genom att följa icke-matchningsbågar åt höger och matchningsbågar åt vänster som figuren nedan visar, tills dess att en omatchad nod på högersidan hittas, vilket innebär en augmenting path. Då gör man färdigt alla noder på samma "avståndsnivå" så att man säkert har fått med alla augmenting paths med minimal längd (3 i exemplet nedan). Sedan gör man en ny sökning av typen DFS, där man begränsar sig till de noder som besöktes i den första sökningen. Man kan tänka sig att man söker i "BFS-trädet", men man behöver inte spara detta explicit. I exemplet kan man t.ex. börja från B och då hitta vägen B2A1 som då direkt kan processas och noderna markeras som tagna. När man sedan fortsätter DFS-sökningen från D hittar man D3C4 och när även denna har processats ser matchningen ut som till höger, den är naturligtvis redan maximal.

Nu kan man ju invända att vi hade tur som hittade B2A1-vägen
först. Eftersom besöksordningen i DFS är helt godtycklig kunde
vi lika gärna ha börjat med att hitta D2A1-vägen och
när sedan sökningen fortsätter från B så
tar det stopp direkt eftersom 2 redan är besökt. I detta
fall hittas bara en augmenting path i detta steg och matchningen kommer inte
ännu att vara maximal, utan en ny sökning måste göras
för att hitta en ytterligare augmenting path, nämligen B2D3C4
. Emellertid lyckades Hopcroft och Karp bevisa att även om man inte
hittar maximalt antal augmenting paths varje gång, utan endast garanterar
att det inte finns någon ytterligare augmenting path i BFS-trädet
när man har processat några godtyckliga vägar, så reduceras
antalet utökningssteg från V till O(sqrt(V)) . Eftersom
både BFS och DFS går på O(E) tid, så blir
komplexiteten för hela algoritmen
O(E sqrt(V))