Varför dokumenterar man kod? Måste man alltid dokumentera kod? Om man vet att koden man skriver ska köras mer än en gång av någon annan än en själv behövs någon form av dokumentation. I stora system finns flera typer av dokumentation som ska skrivas.
Man skriver ofta kommentarer i programkod. Väl skött är den ovärderlig vid själva utvecklingen. I ett större projekt med många inblandade kan inte alla ta del av all kod eller ens någon kod alls. Därför måste också ytterligare dokumentation skrivas.
System som inte är dokumenterade går varken att använda eller underhålla. Vid slutlig leverans måste systemet vara fullständigt dokumenterat. Det är inte bara slutanvändaren som behöver dokumentation. Även inom projektet behöver olika komponenter, kod, delsystem och utvecklingsverktyg dokumenteras. Tänk på att den kod du skriver kanske behöver underhållas i flera decennier framöver.
Det finns många olika typer av dokumentation som skrivs före, under och efter ett stort mjukvaruprojekt. Exakt vilka som används skiljer sig naturligtvis lite mellan olika organisationer och projekt. Här är några typer som ofta finns med:
Dokumentationen utgör ofta beslutsunderlag till om projektet ska få fortsätta eller om det överhuvudtaget ska få starta. Naturligtvis används dokument även vid mindre beslut.
I Python skriver man funktionskommentarer (och klasskommentarer) direkt efter deklarationen. Man skriver kommentaren som en vanlig flerradssträng (inleds och avslutas med tre citattecken), till exempel:
"""
En modul för schemahantering
081009/linda
"""
def skriv_schema(schemat):
"""
Funktionen skriver ut schemat på stdout
schemat - en dictionary som innehåller schemat
"""
.
.
.
Med modulen pydoc Från terminalfönstret kan man också skriva ut dokumentationen:
dator>pydoc ./schema.pyObservera att det måste finnas med ett snedstreck i sökvägen (annars söker pydoc efter befintlig dokumentation istället).
Väljaren -w ger en html-fil (schema.html) med samma information.
dator>pydoc -w ./schema.py
Att testa sina program är en självklarhet, annars vet man ju inte om de fungerar. Det är en sak att få sitt program att kompilera, en annan att sak att det verkligen gör det man vill att det ska göra.
Det är väldigt svårt att veta om man testat allt.
Det finns en modul i python - doctest - som kan tolka tester i kodkommentaren. Man kan klistra in en testkörning av funktionen och den kommer att utföras. Här följer ett exempel på get()-funktionen i en köklass (se labb 2).
class Queue:
"En köklass"
# Kod i köklassen
def get(self):
"""
Returnerar och tar bort det som står först i kön.
>>> q = Queue()
>>> q.put(5)
>>> q.put(3)
>>> q.get() == 5
True
"""
# Här börjar koden i funktionen
x = self.first.value
self.first = self.first.next
return x
# Mer kod i köklassen
def _test():
import doctest
doctest.testmod()
if __name__ == "__main__":
_test()
Kör vi funktionen _test() får vi en utmatning som berättar vilka tester som görs. Vore köklassen felaktigt implementerad så get() returnerade något annat än 5 skulle vi få följande svar:
**********************************************************************
File "queue.py", line 22, in __main__.Queue.get
Failed example:
q.get == 5
Expected:
True
Got:
False
**********************************************************************
1 items had failures:
1 of 4 in __main__.Queue.get
***Test Failed*** 1 failures.
Det behövs många tester för att testa stora system och alla dessa går inte att skriva i kodkommentarer för då blir inte kommentaren läslig. Istället skriver man egna testklasser som bara har till uppgift att testa en eller flera klasser i systemet. För att testa igenom hela systemet kör man sedan alla testfall i alla testklasser. I python finns ett paket - unittest - som man använder för detta.
Ett viktigt skäl till testning är att göra regressionstest, d.v.s. att kontrollera att den befintliga koden inte påverkas i oönskad riktning då man tillför eller ändrar någon annanstans. Om systemet är stort medför det ofta att många tusentals test måste göras varje gång något ändras i koden. Att automatisera testningen är nödvändigt.
Odokumenterade tester är värdelösa! Får man under utvecklingen av ett system en felrapport från ett test måste man snabbt kunna få veta vad för slags fel det är, helst så noggrant beskrivet som möjligt. All testkod måste alltså också dokumenteras så det är lätt att felsöka.
Det är inte obligatoriskt att skriva ett program för automattestning av labb 6. Men det rekommenderas varmt - här finns det nämligen många olika fall att ta hänsyn till och det är tidsödande att provköra programmet för hand efter varje ändring.
Olika former av kryptering har använts så länge man har velat ha skriftliga hemligheter. Redan dom gamla grekerna hade flera system för kryptering.
Samma effekt kan vi få genom att skriva meddelandet i en mxn-matris och bilda det kodade meddelandet genom att ta varje kolumn i texten. Den som känner till matrisens storlek kan lätt avkoda det. Man brukar skippa mellanslag och skiljetecken för att göra det svårare att knäcka koden.
JAGGÖ MMERP ENGAR NAIDE NGAML AEKENkodas alltså som:
JMENNAAMNAGEGEGIAKGRADMEÖPRELN
En variant är rot13 där man förskjuter varje bokstav 13 steg. Hamnar man utanför alfabetet roterar man runt till början igen.
def rot13(meddelande):
alfabet = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
kod = ""
for bokstav in meddelande:
index = (alfabet.find(bokstav) + 13) % 26
kod = kod + alfabet[index]
return kod
Om vi skippar ÅÄÖ får vi ett alfabet som består av 26 tecken,
vilket innebär att vi kan använda samma funktion för dekryptering!
rot13("HEMLIGHETER") blir URZYVTURGRE
rot13("URZYVTURGRE") blir HEMLIGHETER
Ännu hemligare blir det om vi slumpar fram en mappning
istället för att flytta fram ett visst antal steg.
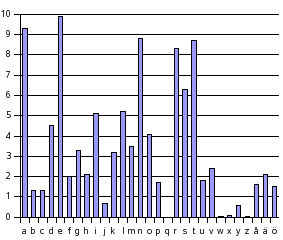
ABCDEFGHIJKLMNOPQRSTUVWXY ||||||||||||||||||||||||| FSXNVDQBCULRHKTPAOMWJEIGYAlla dessa chiffer är dock enkla att knäcka om man har statistik över hur ofta varje bokstav förekommer i det aktuella språket. Så här ser det ut för svenska:
Krypteringsalgoritmen RSA (döpt efter Ron Rivest, Adi Shamir och Leonard Adleman som först publicerade den) löser detta genom att ha en offentlig nyckel och en privat nyckel. Den offentliga nyckeln delar du ut till alla, så att dom kan kryptera meddelanden och skicka till dig, men det är bara du som kan dekryptera med hjälp av den privata nyckeln.
Först måste vi beräkna nycklarna:
Sedan beräknar vi mie modulo n för att få de kodade delarna ci.
Den som vill dekryptera måste känna till d, och kan då få ut det ursprungliga meddelandet genom att beräkna cid modulo n för varje ci.
Här finns en demonstration av RSA. Prova t ex att kryptera Power Rangers hemliga kod Galwit Mysto Prifior.
För att knäcka RSA måste man faktorisera n, dvs lista ut vilka de två stora primtalen p och q är. Det finns ännu ingen algoritm som kan göra detta i polynomisk tid, dvs O(Lk) där L är längden av primtalet och k är en godtycklig konstant, vilket innebär att beräkningen tar för lång tid för att vara praktiskt användbar. Därför räknar man med att RSA i nuläget är oknäckbar för tillräckligt stora primtal.
En fortsättningskurs som bland annat handlar om tillämpningar av kryptering är DD2395 Datasäkerhet. Där får man också lära sig om t ex virus och datajuridik.
Säkerhetsaspekter tas även upp i kursen DD1334 Databasteknik som vissa av er läser redan i vår.
Vi har förstås också kursen DD2449 Kryptografins grunder (men den kräver att man läst DD1352 ADK först).