Path Clustering with Homology Area

This page provides some supplemental material on the the paper homology clustering (pdf available here). A live notebook example can be consulted in github

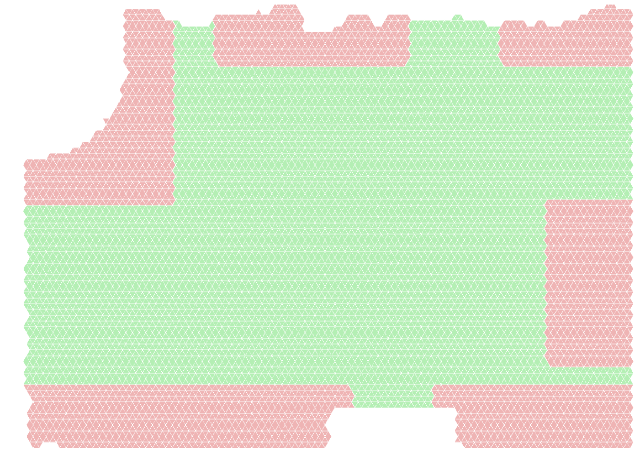
In here we go a little bit deeper into the processing of the paths in the Edinburgh Informatics forum Pedestrian Dataset. To begin with, in our tests, we extracted a set of 2000 paths. In the current framework, we use boxes which are parametrized with a lower and/or upper bound to the coordinates $x$ and $y$ to define the part of the space that is going to be quotiented. We chose the following bounds, as they encompass (most of) the end-points of paths in the dataset.

• $x < 150 , 250 < y$
• $200 < x < 400 , 400 < y$
• $500 < x , 400 < y$
• $x < 340 , y < 60$
• $430 < x , y < 60$
• $550 < x , 80 < y < 250$

With that in place we approximate the space with a regular simplicial complex $S$ where every triangle has a side of length 7 to obtain the following triangulation (right).

Now, using this triangulated region we compute the distance matrix of the set of paths using our method. Doing this results in the following times (using our python implementation with a single core of an intel core i7 processor).

number of bounding chains calculated: 15498
this number includes some non-homologous paths
time calculating bounding chains: 1187.261066 s
number of combinations computed: 171899
time calculating combinations: 42.101311 s
number of paths from different hom clusters: 1465246
this is the number of bounding chains we did not have to compute

Roughly speaking, these numbers show how much time is saved by using our algorithm (Algorithm 2 in the paper) to compute the distance array.

Comparing times with DTW and FastDTW

Recall, from the paper, that the only reason that we can compute the distance using (Algorithm 2) is that subtracting the bounding between paths $p,q$ from the bounding chain between $p,q’$ produces the bounding chain, between $q,q’$. These gains were quantified in the previous section, and we can use timing information to compare with DTW and FastDTW.

	DTW	fastDTW	MARHom
Average Time (ms)	12	3	83
Total Naive Time (h:m)	6:39	1:39	46:05

These Average Times refer to the average time to compute the distance between two paths in the Edinburgh Path Dataset using the different methods, the Total Naive Times refer to the total time needed to compute a distance array for a set 2000 paths, extrapolated from the average times (i.e. $1999000 \times$Average Time¹).

However, converting the timing information from calculating the distance array (quoted in the previous section) we had:

time calculating bounding chains: 1187.261066 s
time calculating combinations: 42.101311 s

Which comes down to 20 minutes, whereas DTW and FastDTW, cannot benefit from the same optimizations. However, we should also compare the output of our method with that of DTW and FastDTW.

Comparing clusters with DTW and FastDTW

To compare the outputs we decided to choose a single homology cluster ². bellow are the paths of this cluster depicted in yellow over the grid.

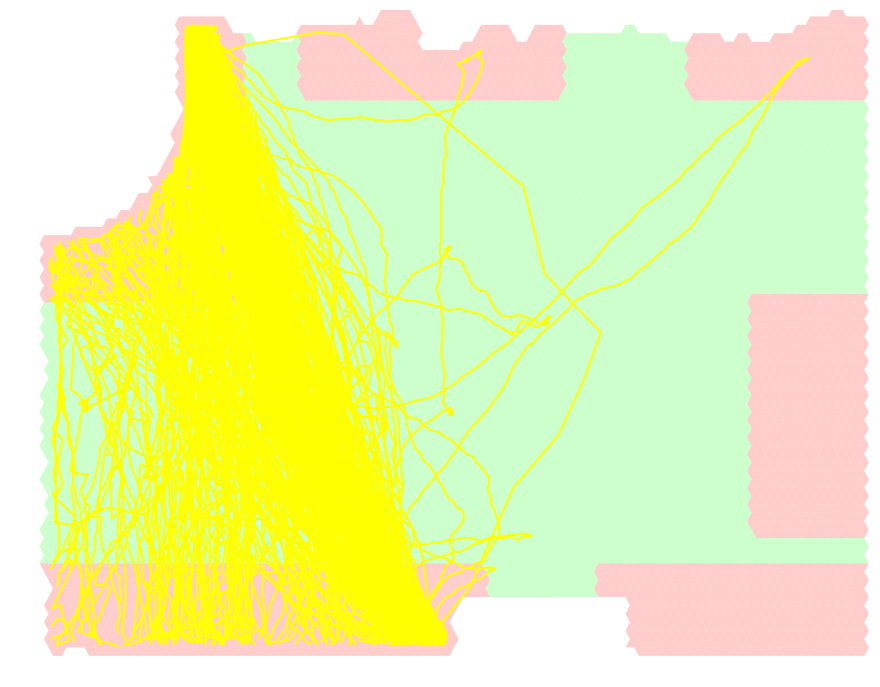
In order to infer the proper distance threshold for clustering, we employed complete linkage clustering on this set of paths which gave us the following dendrograms:

MARHom	DTW

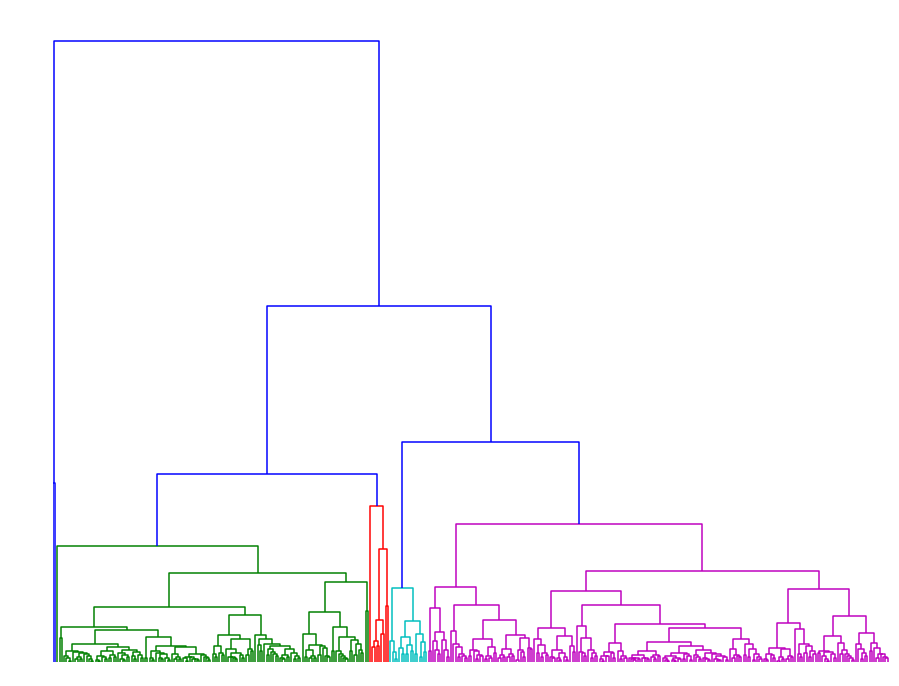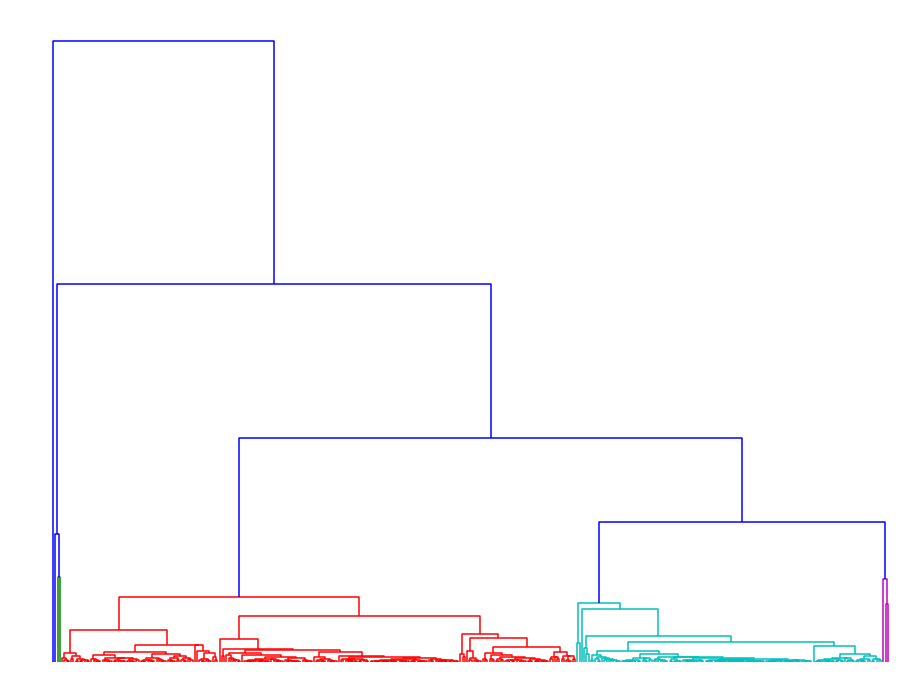The dendrogram on the left corresponds to our method, whereas the one on the right corresponds to using DTW on this homology cluster. The color threshold was chosen so that the dendrogram would yield 5 clusters.

Simply from comparing the dendrograms we see that DTW already clusters paths together at very low thresholds.

MARHom	DTW

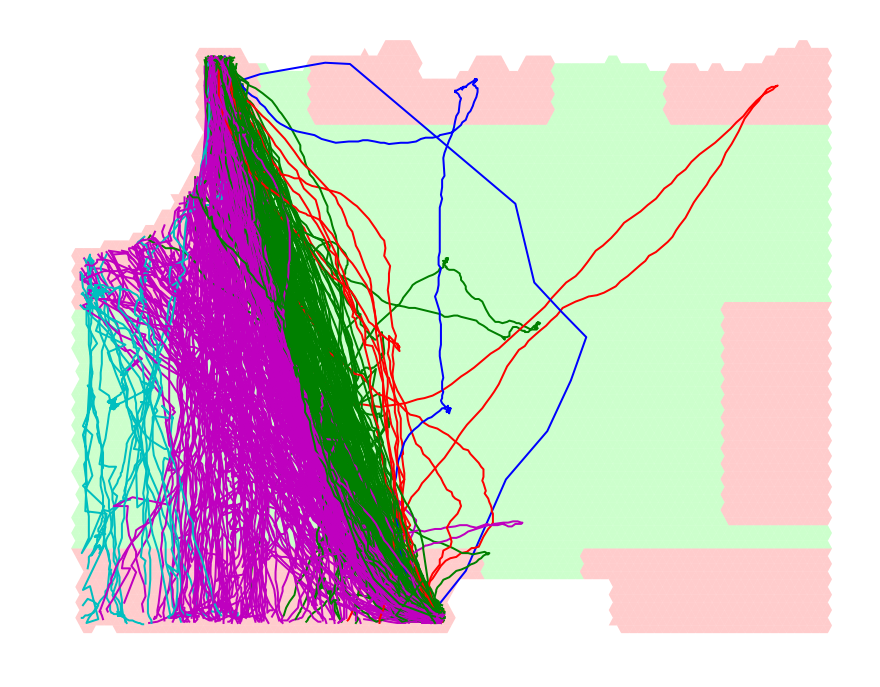
By looking at the clustering in the picture above we see that DTW, for some reason, produces a very large cluster (in red) that seems to be broken by another cluster (in light-blue). Our method, on the other hand, produces mostly spacially-coherent clusters.

---