MINIMUM METRIC TRAVELING K-SALESPERSON PROBLEM

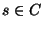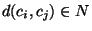• INSTANCE: Set C of m cities, an initial city $s\in C$, distances $d(c_i,c_j)\in N$ satisfying the triangle inequality.

• SOLUTION: A collection of k subtours, each containing the initial city s, such that each city is in at least one subtour.

• MEASURE: The maximum length of the k subtours.

  
  

• Good News: Approximable within 1-1/k plus the performance ratio of the MINIMUM METRIC TRAVELING SALESPERSON PROBLEM, i.e., within 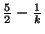$\frac{5}{2}-\frac{1}{k}$ [171].

• Comment: The non-metric variation in which the graph is a tree and k possibly different initial cities are given in the input is approximable within 2-2/(p+1) [48].