



Next: MINIMUM CHINESE POSTMAN FOR
Up: Routing Problems
Previous: MINIMUM METRIC TRAVELING K-SALESPERSON
Index
- INSTANCE:
Set C of m cities, an initial city
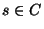 ,
a final city
,
a final city 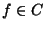 ,
distances
,
distances
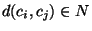 satisfying the triangle inequality.
satisfying the triangle inequality.
- SOLUTION:
A simple path from the initial city s to the final city f passing through
all cities in C, i.e., a permutation
![$\pi: [1..m]\rightarrow[1..m]$](img411.gif) such that
such that 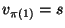 and
and 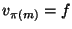 .
.
- MEASURE:
The length of the largest distance in the path, i.e.,
- Good News:
Approximable within 2 [254].
- Bad News:
Not approximable within 2
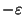 for any
for any
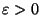 [254].
[254].
- Comment:
The same positive and negative results hold even if X is a set of point in
d-dimensional space with the
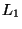 or
or 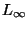 metric. If the
metric. If the 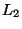 metric
is used then the upper bound is 1.969 [152].
The corresponding maximization problem called MAXIMUM SCATTER TSP, where
the length of the shortest distance in the path is maximized, is approximable
within 2, but not approximable within
metric
is used then the upper bound is 1.969 [152].
The corresponding maximization problem called MAXIMUM SCATTER TSP, where
the length of the shortest distance in the path is maximized, is approximable
within 2, but not approximable within 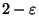 for any
for any
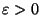 [26].
[26].
- Garey and Johnson: ND24




Next: MINIMUM CHINESE POSTMAN FOR
Up: Routing Problems
Previous: MINIMUM METRIC TRAVELING K-SALESPERSON
Index
Viggo Kann
2000-03-20
![\begin{displaymath}\max\limits_{i\in[1..m-1]}d\left(\{c_{\pi(i)},c_{\pi(i+1)}\}\right).\end{displaymath}](img430.gif)
![\begin{displaymath}\max\limits_{i\in[1..m-1]}d\left(\{c_{\pi(i)},c_{\pi(i+1)}\}\right).\end{displaymath}](img430.gif)