MINIMUM MULTIPROCESSOR SCHEDULING

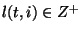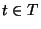• INSTANCE: Set T of tasks, number m of processors, length $l(t,i)\in Z^+$ for each task $t\in T$ and processor $i\in [1..m]$.

• SOLUTION: An m-processor schedule for T, i.e., a function $f: T\rightarrow[1..m]$.

• MEASURE: The finish time for the schedule, i.e., $\max\limits_{i\in[1..m]}\displaystyle\sum\limits_{t\in T: \atop f(t)=i} l(t,i)$.

  
  

• Good News: Approximable within 2 [348].

• Bad News: Not approximable within 3/2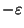$-\varepsilon$ for any $\varepsilon >0$ [348].

• Comment: Admits an FPTAS for the variation in which the number of processors m is constant [261]. Admits a PTAS for the uniform variation, in which l(t,i) is independent of the processor i [255]. A variation in which, for each task t and processor i, a cost c(t,i) is given in input and the goal is to minimize a weighted sum of the finish time and the cost is approximable within 2 [441]. Variation in which each task has a nonnegative penalty and the objective is to minimize the finish time for accepted jobs plus the sum of the penalties of rejected jobs, is approximable within 2-1/m and admits an FPTAS for fixed m [64].

• Garey and Johnson: Generalization of SS8