



Next: MINIMUM RESOURCE CONSTRAINED SCHEDULING
Up: Multiprocessor Scheduling
Previous: MINIMUM MULTIPROCESSOR SCHEDULING
Index
- INSTANCE:
Set T of tasks, each having length l(t)=1, number m of processors, and
a partial order < on T.
- SOLUTION:
An m-processor schedule for T that obeys the precedence constraints, i.e., a
function
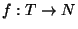 such that, for all
such that, for all 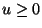 ,
,
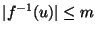 and such that t < t' implies f(t') > f(t).
and such that t < t' implies f(t') > f(t).
- MEASURE:
The finish time for the schedule, i.e.,
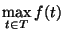 .
.
- Good News:
Approximable within
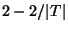 [344].
[344].
- Bad News:
Not approximable within 4/3
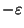 for any
for any
 [346].
[346].
- Comment:
A variation with an enlarged class of allowable constraints is approximable
within
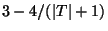 while a variation in which the partial order < is
substituted with a weak partial order
while a variation in which the partial order < is
substituted with a weak partial order 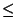 is approximable within
is approximable within
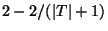 [71].
Variation in which there is a communication delay of 1, i.e., if two tasks
t<t' are scheduled on different machines, then f(t')>f(t)+1,
is approximable within 3 [422],
and not approximable within 5/4
[71].
Variation in which there is a communication delay of 1, i.e., if two tasks
t<t' are scheduled on different machines, then f(t')>f(t)+1,
is approximable within 3 [422],
and not approximable within 5/4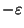 [260].
The same problem without limit on the number of processors, i.e. with
[260].
The same problem without limit on the number of processors, i.e. with
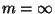 ,
is not approximable within 7/6
,
is not approximable within 7/6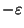 [260].
The variation of this problem in which the average weighted completion
time has to be minimized is approximable within 10/3 (respectively,
6.143 if the tasks have arbitrary length) [379].
Generalization where the tasks have lengths l(t) and the processors have
speed factors s(i) is approximable within
[260].
The variation of this problem in which the average weighted completion
time has to be minimized is approximable within 10/3 (respectively,
6.143 if the tasks have arbitrary length) [379].
Generalization where the tasks have lengths l(t) and the processors have
speed factors s(i) is approximable within 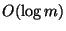 [115].
[115].
- Garey and Johnson: SS9




Next: MINIMUM RESOURCE CONSTRAINED SCHEDULING
Up: Multiprocessor Scheduling
Previous: MINIMUM MULTIPROCESSOR SCHEDULING
Index
Viggo Kann
2000-03-20