Comment:
For any prime 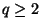 the problem over GF[q] is approximable within q, but
is not approximable within
the problem over GF[q] is approximable within q, but
is not approximable within 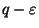 for any
for any
 ,
even if the
number of variables in each equation is exactly three.
When there are at most two variables in each equation the problem
over GF[2] is approximable within 1.383 but is not approximable within
1.0909 [242];
not approximable within 1.0030 if the number of occurrences of any variable
is bounded by 3 [76].
When there are at most two variables in each equation the problem
over GF[q] for any prime
,
even if the
number of variables in each equation is exactly three.
When there are at most two variables in each equation the problem
over GF[2] is approximable within 1.383 but is not approximable within
1.0909 [242];
not approximable within 1.0030 if the number of occurrences of any variable
is bounded by 3 [76].
When there are at most two variables in each equation the problem
over GF[q] for any prime 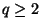 is approximable within
is approximable within 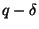 for some
for some 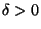 (dependent on q) but not approximable within
70/69
(dependent on q) but not approximable within
70/69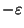 for any
for any
 [22].
When there are exactly k variables in each equation and the number of
equations is
[22].
When there are exactly k variables in each equation and the number of
equations is 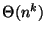 the problem over GF[q] for any prime
the problem over GF[q] for any prime
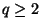 admits a randomized PTAS [21].
admits a randomized PTAS [21].
The variation in which the system consists of relations (> or 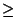 )
is
APX-complete and approximable within 2
[16].
If the variables are restricted to assume only binary values, the problem is
harder to approximate than MAXIMUM INDEPENDENT SET.
Approximability results for even more variants of the problem can be found in
[16].
)
is
APX-complete and approximable within 2
[16].
If the variables are restricted to assume only binary values, the problem is
harder to approximate than MAXIMUM INDEPENDENT SET.
Approximability results for even more variants of the problem can be found in
[16].
![]() )
is
APX-complete and approximable within 2
[16].
If the variables are restricted to assume only binary values, the problem is
harder to approximate than MAXIMUM INDEPENDENT SET.
Approximability results for even more variants of the problem can be found in
[16].
)
is
APX-complete and approximable within 2
[16].
If the variables are restricted to assume only binary values, the problem is
harder to approximate than MAXIMUM INDEPENDENT SET.
Approximability results for even more variants of the problem can be found in
[16].