



Next: MAXIMUM HYPERPLANE CONSISTENCY
Up: Mathematical Programming
Previous: MAXIMUM SATISFYING LINEAR SUBSYSTEM
Index
- INSTANCE:
System Ax=b of linear equations, where A is an integer
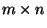 -matrix, and b is an integer m-vector.
-matrix, and b is an integer m-vector.
- SOLUTION:
A rational n-vector
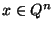 .
.
- MEASURE:
The number of equations that are not satisfied by x.
- Bad News:
Not in APX [35].
- Comment:
Not approximable within
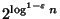 for any
for any
 unless NP
unless NP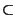 QP [35].
If the system consists of relations (> or
QP [35].
If the system consists of relations (> or 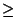 )
the problem is even
harder to approximate; there is a transformation from
MINIMUM DOMINATING SET to this problem.
If the variables are restricted to assume only binary values the problem is
NPO PB-complete both for equations and relations, and is not approximable
within
)
the problem is even
harder to approximate; there is a transformation from
MINIMUM DOMINATING SET to this problem.
If the variables are restricted to assume only binary values the problem is
NPO PB-complete both for equations and relations, and is not approximable
within
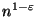 for any
for any
 .
Approximability results for even more variants of the problem can be found in
[17].
.
Approximability results for even more variants of the problem can be found in
[17].
Viggo Kann
2000-03-20