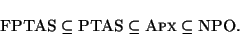Approximate algorithms and approximation classes

It is well-known that if an NPO problem can be solved in polynomial time, then its corresponding decision problem can also be solved in polynomial time. As a consequence, if $\mbox{\sc P}\neq NP$, then any NPO problem whose corresponding decision problem is NP-complete is not solvable in polynomial time. In these cases we sacrifice optimality and start looking for approximate solutions computable in polynomial time.

Definition 2  

Let A be an NPO problem. Given an instance x and a feasible solution y of x, we define the performance ratio of y with respect to x as

$$R(x,y) = \max\left\{\frac{m(x,y)}{\mbox{\sl opt}(x)}, \frac{\mbox{\sl opt}(x)}{m(x,y)}\right\}.$$

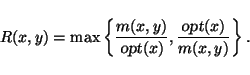
The performance ratio is always a number greater than or equal to 1 and is as close to 1 as y is close to the optimum solution.

Definition 3  

Let A be an NPO problem and let T be an algorithm that, for any instance x of A, returns a feasible solution T(x) of x. Given an arbitrary function $r: N \rightarrow (1,\infty)$, we say that T is an r(n)-approximate algorithm for A if, for any instance x, the performance ratio of the feasible solution T(x) with respect to x verifies the following inequality:

$$R(x,T(x)) \leq r(\vert x\vert).$$

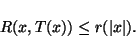
If an NPO problem admits an r(n)-approximate polynomial-time algorithm we say that it is approximable within r(n).

Definition 4  

An NPO problem A belongs to the class APX if it is approximable within $\varepsilon$, for some constant $\varepsilon > 1$.

Definition 5  

Let A be an NPO problem. An algorithm T is said to be an approximation scheme for A if, for any instance x of A and for any rational $\varepsilon > 1$, $T(x, \varepsilon )$ returns a feasible solution of x whose performance ratio is at most $\varepsilon$.

Definition 6  

An NPO problem A belongs to the class PTAS if it admits a polynomial-time approximation scheme, that is, an approximation scheme whose time complexity is bounded by q(|x|) where q is a polynomial.

Observe that the time complexity of an approximation scheme in the above definition may be of the type $2^{1/(\varepsilon -1)}p(\vert x\vert)$ or $\vert x\vert^{1/(\varepsilon -1)}$ where p is a polynomial. Thus, computations with $\varepsilon$ values very close to 1 may turn out to be practically unfeasible. This leads us to the following definition.

Definition 7  

An NPO problem A belongs to the class FPTAS if it admits a fully polynomial-time approximation scheme, that is, an approximation scheme whose time complexity is bounded by $q(\vert x\vert, 1/(\varepsilon -1))$ where q is a polynomial.

Clearly, the following inclusions hold:

$$\mbox{\sc FPTAS}\subseteq \mbox{\sc PTAS}\subseteq \mbox{\sc Apx}\subseteq \mbox{\sc NPO}.$$

It is also easy to see that these inclusions are strict if and only if $\mbox{\sc P}\neq NP$.