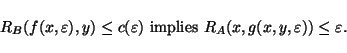Next: A list of NPO
Up: Introduction
Previous: Approximate algorithms and approximation
Index
Completeness in approximation classes
In this section we define a natural approximation preserving reducibility
and introduce the notion of completeness both in NPO and in APX.
Definition 8
Let A and B be two NPO problems. A is said to be PTAS-reducible to B, in symbols
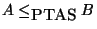 ,
if three functions
f, g, and c exist such that:
,
if three functions
f, g, and c exist such that:
- 1.
- For any
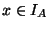 and for any rational
and for any rational
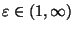 ,
,
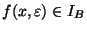 is computable in time polynomial with respect to
|x|.
is computable in time polynomial with respect to
|x|.
- 2.
- For any
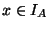 ,
for any
,
for any
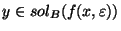 ,
and for any
rational
,
and for any
rational
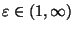 ,
,
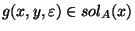 is computable
in time polynomial with respect to both |x| and |y|.
is computable
in time polynomial with respect to both |x| and |y|.
- 3.
-
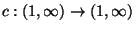 is computable and invertible.
is computable and invertible.
- 4.
- For any
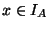 ,
for any
,
for any
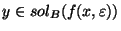 ,
and for any
rational
,
and for any
rational
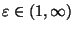 ,
,
Remark 1
In [393] a different kind of reducibility between optimization
problems is defined which is called L-reducibility. It is possible to prove
that, within APX, the L-reducibility is a restriction of the
PTAS-reducibility [127]. More recently, another restriction of
the PTAS-reducibility, called E-reducibility, has been introduced in
[305].
Definition 9
A problem
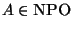 is NPO-complete if, for any
is NPO-complete if, for any
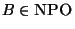 ,
,
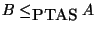 .
.
Definition 10
A problem
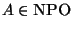 is APX-hard if, for any
is APX-hard if, for any
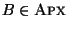 ,
,
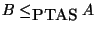 .
An APX-hard problem is APX-complete if it belongs to APX.
.
An APX-hard problem is APX-complete if it belongs to APX.
From Proposition 1
it immediately follows that if an NPO problem A is
NPO-complete (respectively, APX-hard) then it does not belong to APX
(respectively, PTAS). It is also possible to prove that if A is
NPO-complete (respectively, NPO PB-complete) then it cannot be approximated
within
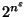 (respectively,
(respectively, 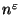 )
for some
)
for some
 .
.
The syntactically defined classes MAX SNP (containing e.g.
MAXIMUM 3-SATISFIABILITY and MAXIMUM CUT) and MAX NP (containing e.g. MAXIMUM SATISFIABILITY)
were defined in [393].
Recently was shown that the closures of these
classes under PTAS-reduction were identical to APX [305] and [129]. In the compendium we
therefore always use the term APX-complete instead of MAX
SNP-complete and APX-hard instead of MAX SNP-hard.
The classes MAX PB and MIN PB consisting of the
polynomially bounded maximization and minimization problems,
respectively, were defined in [329]. The closures of these
classes under PTAS-reduction have recently been shown to be identical
to NPO PB [125]. In the compendium we therefore
always use NPO PB-complete instead of MAX PB-complete and MIN PB-complete.




Next: A list of NPO
Up: Introduction
Previous: Approximate algorithms and approximation
Index
Viggo Kann
2000-03-20
![]() ,
if three functions
f, g, and c exist such that:
,
if three functions
f, g, and c exist such that:
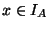 and for any rational
and for any rational
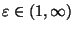 ,
,
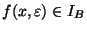 is computable in time polynomial with respect to
|x|.
is computable in time polynomial with respect to
|x|.
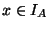 ,
for any
,
for any
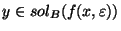 ,
and for any
rational
,
and for any
rational
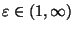 ,
,
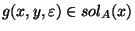 is computable
in time polynomial with respect to both |x| and |y|.
is computable
in time polynomial with respect to both |x| and |y|.
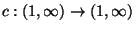 is computable and invertible.
is computable and invertible.
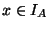 ,
for any
,
for any
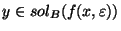 ,
and for any
rational
,
and for any
rational
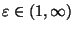 ,
,