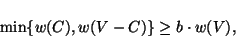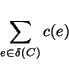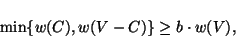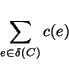Next: MINIMUM B-VERTEX SEPARATOR
Up: Cuts and Connectivity
Previous: MINIMUM RATIO-CUT
Index
- INSTANCE:
Graph
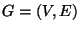 ,
a vertex-weight function
,
a vertex-weight function
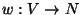 ,
an
edge-cost function
,
an
edge-cost function
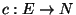 ,
and a rational b,
,
and a rational b, 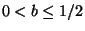 .
.
- SOLUTION:
A cut C, i.e., a subset
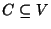 ,
such that
,
such that
where w(V') denotes the sum of the weights of the vertices in V'.
- MEASURE:
The weight of the cut, i.e.,
where
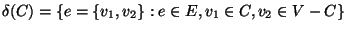 .
.
- Bad News:
Not approximable within
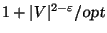 for any
for any
 [93].
[93].
- Comment:
Also called Minimum b-Edge Separator.
There is a polynomial algorithm that finds a b-balanced cut within an
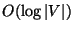 factor of the optimal
factor of the optimal 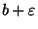 -balanced cut for
-balanced cut for 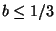 [439].
Approximable within 2 for planar graphs for
[439].
Approximable within 2 for planar graphs for 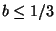 if the vertex weights are polynomially bounded [187].
Not approximable within
if the vertex weights are polynomially bounded [187].
Not approximable within
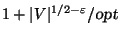 for graphs of
maximum degree 3 [93].
The unweighted problem admits a PTAS if every vertex has degree
for graphs of
maximum degree 3 [93].
The unweighted problem admits a PTAS if every vertex has degree
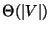 for
for 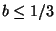 [39].
MINIMUM K-MULTIWAY SEPARATOR, the variation in which the removal of the
cut edges partitions the graph into at most k parts, where the sum of the
vertex weights in each part is at most
[39].
MINIMUM K-MULTIWAY SEPARATOR, the variation in which the removal of the
cut edges partitions the graph into at most k parts, where the sum of the
vertex weights in each part is at most
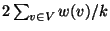 ,
is
approximable within
,
is
approximable within
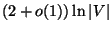 [147].
[147].




Next: MINIMUM B-VERTEX SEPARATOR
Up: Cuts and Connectivity
Previous: MINIMUM RATIO-CUT
Index
Viggo Kann
2000-03-20