Bézier Splines: Continuity
We provide a tool to explore the continuity of Bézier splines interactively on the web. Bézier splines can be created and modified at will. Different continuity conditions can be enforced. Notably, the first and second derivative vectors are visualized to illuminate the connection between their values and the continuity of the spline.
About Bézier Splines and their Continuity
 |
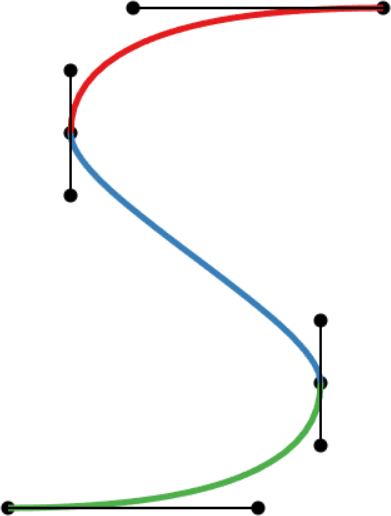 |
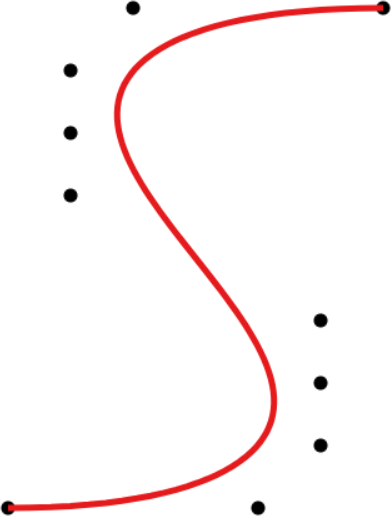
A Bézier curve (left) and a cubic Bézier spline (right) defined by the same set of control points. |
|
Given a control polygon consisting of n + 1 Bézier points, Bézier curves interpolate the first and last point while approximating all other points. They are polynomial curves of degree n. Moving any Bézier point changes the entire curve, i.e., local control is missing.
Bézier splines consist of several Bézier curves that have been joined consecutively. This alleviates the issue of a high polynomial degree and provides local control in most circumstances. Bézier splines can have different levels of continuity at the joint, which can be characterized using the first and second derivative (velocity and acceleration):
- C0-continuity refers to adjacent Bézier curves actually ending and starting at the same point.
- C1-continuity is given when the curve is C0 and the first derivative vectors of both curves coincide at the joint.
- C2-continuity is given when the curve is C0, C1, and the second derivative vectors coincide at the joint.
- G1- and G2-continuity refer to conditions where an appropriate parametrization of the joined curves will achieve C1- or C2-continuity, respectively.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
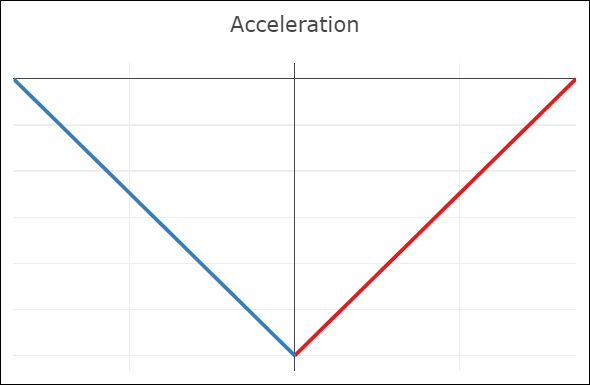 |
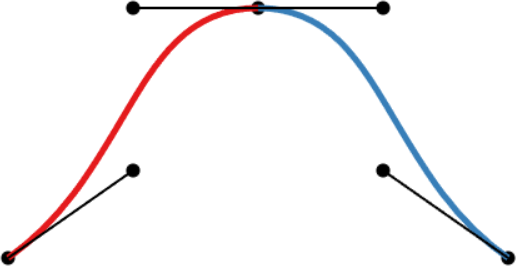
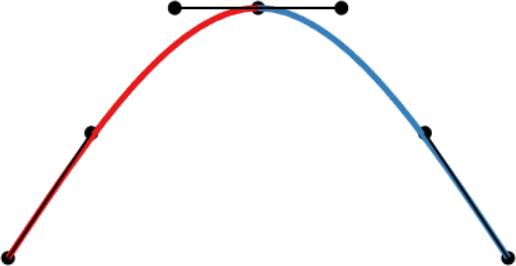
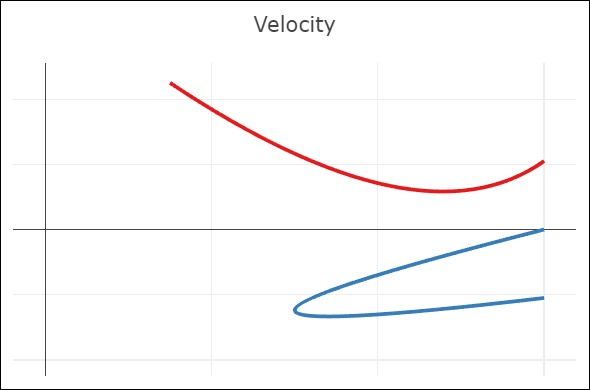
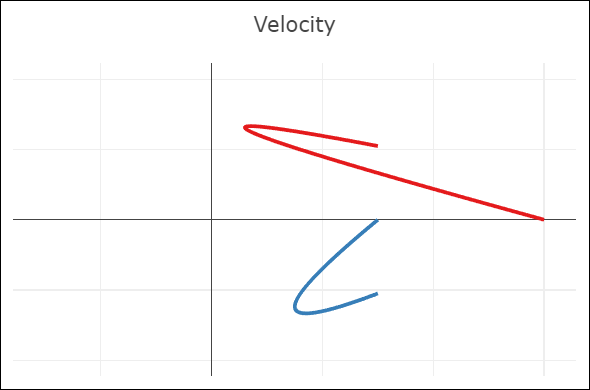
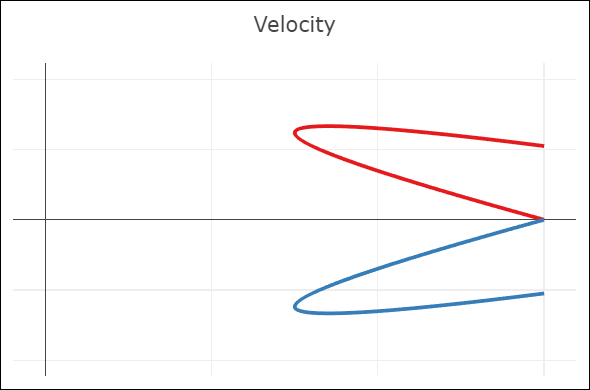
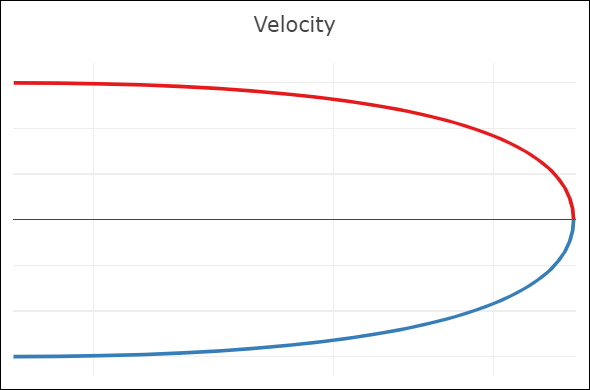
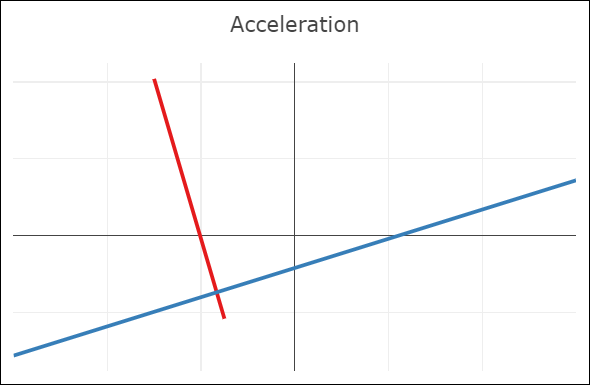
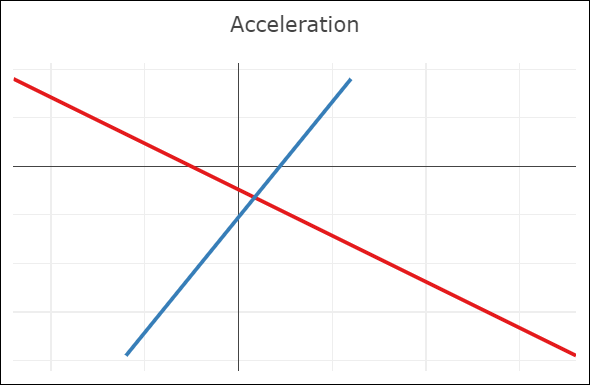
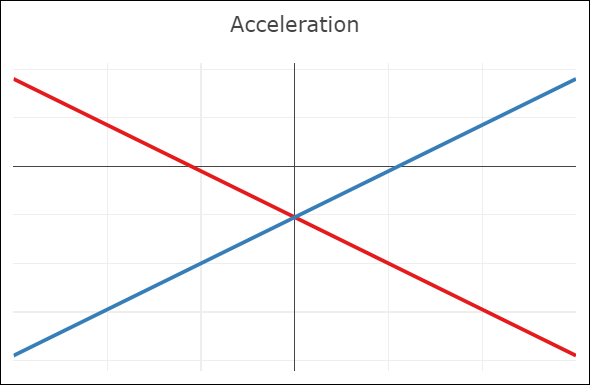
| C0-continuity: continuous curve, discontinuous velocity and acceleration | G1-continuity: continuous curve, semi-discontinuous velocity, discontinuous acceleration | C1-continuity: continuous curve and velocity, discontinuous acceleration | C2-continuity: continuous curve, velocity, and acceleration |
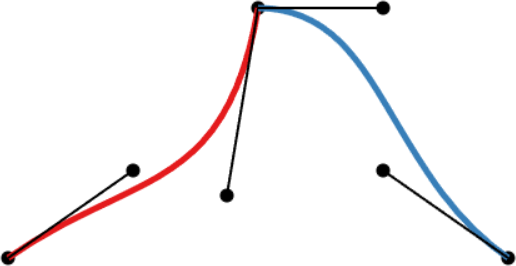
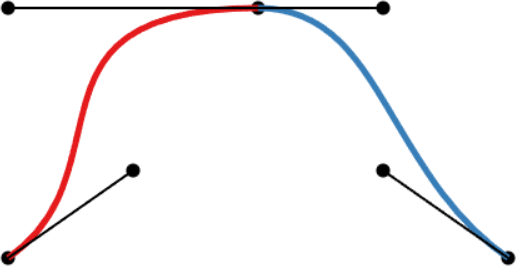
Two cubic Bézier curves joined together to create a spline. The three interpolated points are identical in all examples, but the different positions of the other points allow for different continuity conditions at the joint.
Using the picture from above, we make the following observations:
- A merely C0-continuous joint creates a notable kink in the curve. The velocity plot shows that the first derivatives do not attain the same value at the joint. The same goes for the acceleration (second derivative).
- G1-continuity requires that the directions of the velocity vectors coincide at the joint. This puts mild constraints on the Bézier points before and after the joint: the so-called handles (the black lines around the joint) need to be aligned, but not necessarily of the same length. The velocity plot still shows a discontinuity, but notice how the red derivative ends parallel to the x-axis, and the blue derivative starts parallel to the x-axis. In other words, the derivatives have the same direction, but not length. An appropriate parametrization of the curves (in this case, moving slower through the red curve) leads to the first derivatives being continuous.
- A C1-continuous joint appears visually smooth. The velocity vectors of both Bézier curves coincide at the joint, but not the acceleration vectors.
- A C2-continuous joint is required to achieve smooth animations along the spline, since smooth animations require continuous velocity and acceleration. Note that this restricts the positions of all but the interpolated points. The shown spline uses the so-called natural end condition where the spline reaches zero curvature at its end points. The used knot vector is a simple [0, 1, 2], which means we take the same amount of time to move between adjacent interpolated points.
User Interface
The top of the user interface provides buttons to enforce different continuity conditions. It is also possible to clear all curves, and to show a single Bézier curve (instead of a spline) through all input points.

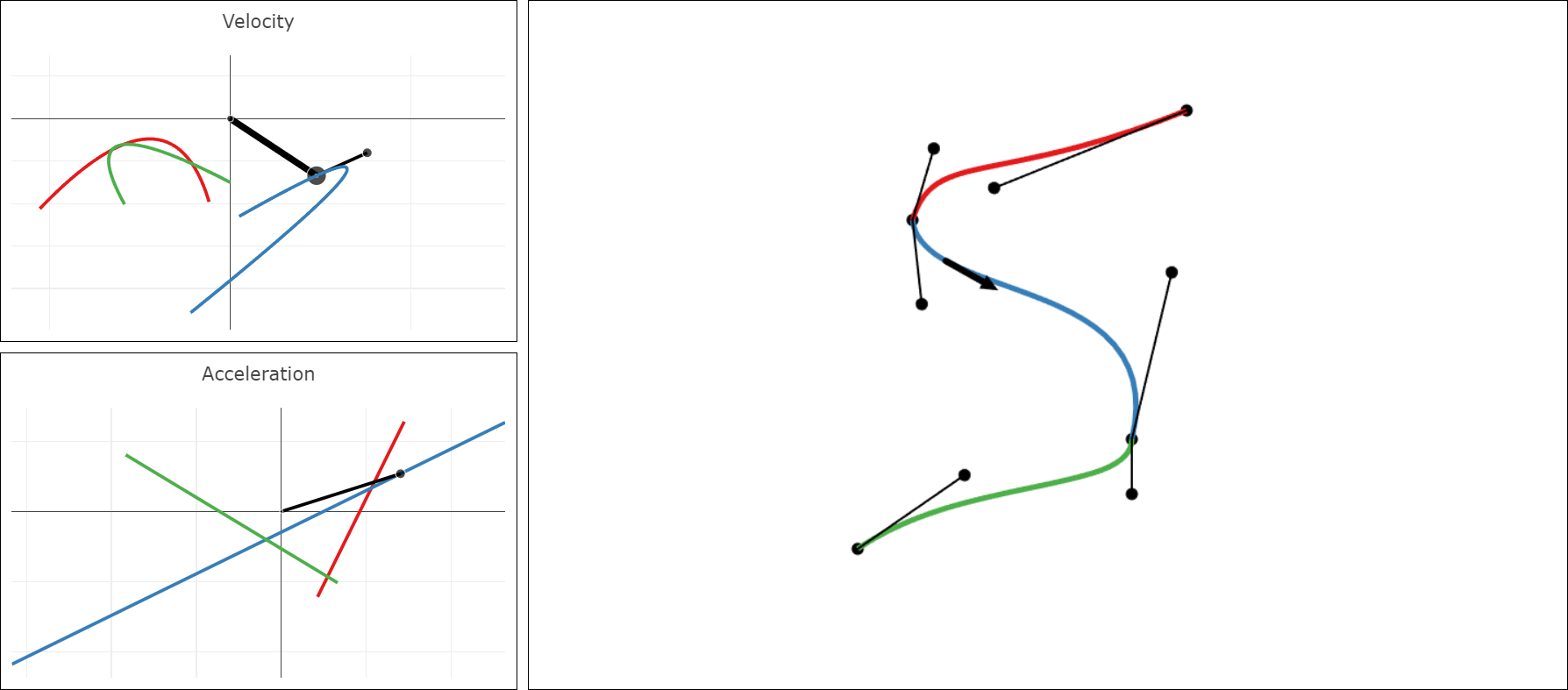
The main part of the user interface provides a large canvas on the right to draw a Bézier spline, and the corresponding velocity and acceleration plots on the left side.
- Click on the canvas to add a point.
- Ctrl-Click on a point to remove it.
- Move a point by dragging it with the left mouse button.
- Hover with the mouse pointer near the spline to see the velocity vector aka. the tangent vector. It is displayed using a black arrow. The same vector is displayed in the velocity plot, where it is anchored at the origin. The velocity plot then also shows its tangent, which is the second derivative of the spline. The acceleration plot shows this vector anchored at the origin.
Authorship and Acknowledgements
This tool has been created by Jule Schmidt and Tino Weinkauf for the course DH2320/DD2258 at KTH Royal Institute of Technology, Stockholm, Sweden.
Our work is inspired by Freya Holmér's video The Continuity of Splines. The setup presented in our tool is similar to what is shown at 20:42 in the video. Note, however, that our C2-continuous spline uses a different setup: we restrict the ends of the spline using the natural end condition, which makes it rather well-behaved. The C2-continuous spline in the video yeets off because the constraints are set differently.
We use Bryce Wilson's code for solving C2 and G2 Bézier splines. The latter are obtained through a knot vector representing the distance ratios between the knots.
We use Plotly to visualize the velocity and acceleration.