3D Flow Around a Confined Square Cylinder
This is a 3D time-dependent flow field. The original data set is 440 GB large and lives on a tetrahedral grid. We provide a much smaller version of about 688 MB here that has been resampled onto a uniform grid. A pre-computed streak line vector field is available for this data set as well.
About the data set
The data set has been obtained from a direct numerical Navier Stokes simulation by Simone Camarri and Maria-Vittoria Salvetti (University of Pisa), Marcelo Buffoni (Politecnico of Torino), and Angelo Iollo (University of Bordeaux I). The used code is a solver for compressible flows on unstructured grids. All details on the code and on the test case can be found in:
S.Camarri, M.-V. Salvetti, M. Buffoni, and A. Iollo. Simulation of the three-dimensional flow around a square cylinder between parallel walls at moderate Reynolds numbers. In XVII Congresso di Meccanica Teorica ed Applicata, 11-15 September 2005, Firenze.
The original data set (440GB, tetrahedral grid) is publicly available from the International CFD Database (defunct).
It is an incompressible solution with a Reynolds number of 200 and the square cylinder has been positioned symmetrically between two parallel walls. The flow has periodic boundary conditions in spanwise direction. It exhibits periodic vortex shedding leading to the well known von Kármán vortex street.
In contrast to most flow data sets, this simulation is initiated from an impulsive start-up and the periodic vortex shedding develops with time. This allows not only to study this interesting phenomenon, but also to evaluate how visualization techniques perform with increasing unsteadiness of the flow.
Visualizations
Smoke Visualization
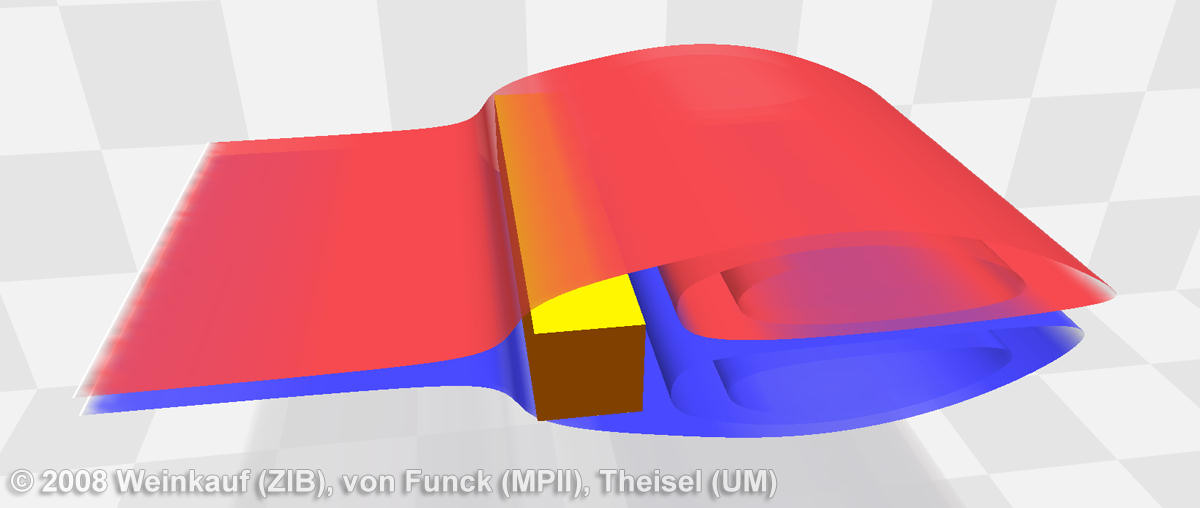
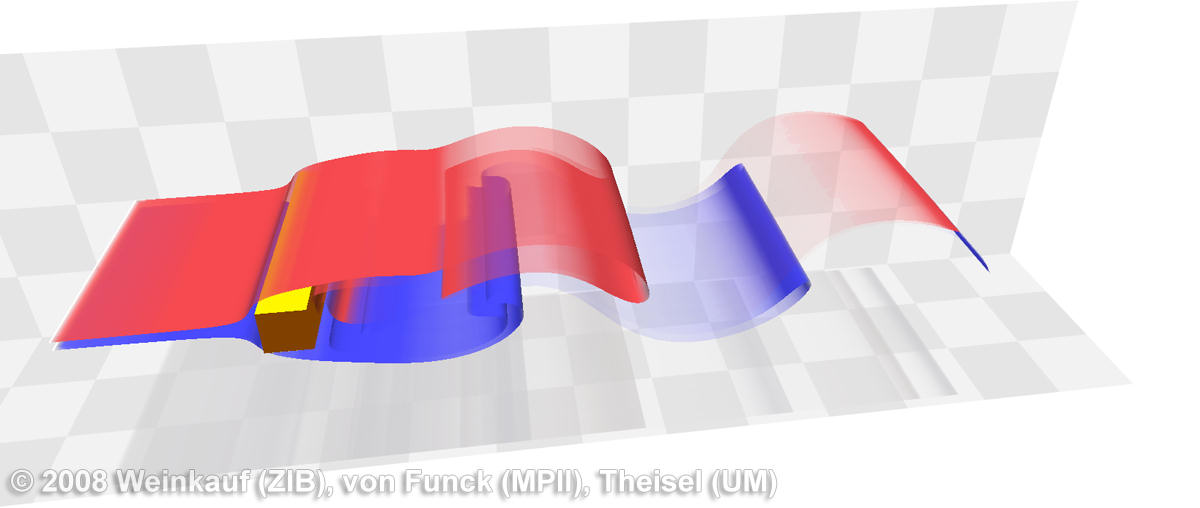
In order to show the alternating behavior of the vortex shedding, we seeded two smoke surfaces (25000 vertices in total) such that the red one passes above the cylinder and the blue one below.
The flow shows a rather steady behavior for the first time steps and the smoke surface develops almost like an ordinary stream surface. In fact, stream and streak surfaces coincide for steady flows. Once the vortex shedding starts, the flow becomes more unsteady - parts of the smoke are ripped off and transported downstream. Note that all the smoke in the figure below is internally represented by two smoke surfaces. This example shows that our alpha computation works reliable even in such challenging situations and produces convincing results. At the end of the transient, the flow develops a von Kármán vortex street with a pronounced three-dimensionality nicely captured by the smoke visualization. We conclude that the visual impression created by smoke surfaces comes closer to real smoke with increasing unsteadiness of a flow.
More information can be found in the paper: Smoke Surfaces: An Interactive Flow Visualization Technique Inspired by Real-World Flow Experiments
 |
 |
 |
 |
Flow behind a square cylinder. Time is increasing from left to right. First the smoke is gathering in a recirculation bubble behind the obstacle. After some time the shedding starts which creates vortices with alternating rotational behavior. Later, the flow develops a pronounced three-dimensionality which can be observed perfectly in the smoke structures. Click on an image to see a larger version.
Streak Surfaces using the Streak Line Vector Field
Here we show two streak surfaces in the flow around the square cylinder. They have been integrated in forward and backward direction from the depicted seeding lines. We computed them using the streak line vector field, which describes streak lines of the original flow as tangent curves. This allows us to compute the streak surfaces as stream surfaces in the derived streak line vector field. The user is able to manipulate the seeding line and gets almost instant feedback in the form of a fully developed streak surface. This way, our new approach provides an interesting, orthogonal alternative to the classic variant for computing streak surfaces: whereas the classic computation scheme focuses on showing the evolution of streak surfaces, the streak line vector field provides quasi-instant results at any given time step. Note that computing a streak surface as a stream surface in the streak line vector field is considerably faster, since one only has to check the front line for adaptivity, whereas the classic approach for streak surfaces requires to check the whole surface for adaptivity.
The pre-computed streak line vector field is available as well.
More information can be found in the paper: Streak Lines as Tangent Curves of a Derived Vector Field
Technical Details
The data set describes a 3D time-dependent flow field and therefore it consists of three components u,v,w specifying the direction of the flow at a certain location in space-time.
Resolution
The data set is given on a 4D uniform grid with the following specifications:
- Grid: 192 x 64 x 48 x 102 (number of grid points in x,y,z,t-direction)
- Bounding Box: [-12, 20] x [-4, 4] x [0, 6] x [0, 162] (extents in x,y,z,t-direction)
Data Format
Each time step is written as a single file in AmiraMesh format. This makes it very easy to apply time-unaware visualization techniques to individual time steps.
Additional Files
In addition to the vector data, the surface of the cylinder itself is provided in the formats Stanford PLY, OpenInventor, and AmiraMesh HyperSurface. The first two formats can be read by almost all mesh processing programs, for example MeshLab.
How to Acknowledge
You are free to use this data set as long as you give proper acknowledgement. Please use a LaTeX snippet similar to the following:
This is a direct numerical Navier Stokes simulation by Simone Camarri and
Maria-Vittoria Salvetti (University of Pisa), Marcelo Buffoni (Politecnico of
Torino), and Angelo Iollo (University of Bordeaux I) \cite{camarri05} which is
publicly available \cite{iCFDDatabase}. We use a uniformly resampled version
which has been provided by Tino Weinkauf and used in von Funck et al.\ for
smoke visualizations \cite{vonfunck08a}.
with the following BibTeX entries:
@INPROCEEDINGS{camarri05,
author = {S.~Camarri and M.-V.~Salvetti and M.~Buffoni and A.~Iollo},
title = {Simulation of the three-dimensional flow around a square cylinder between parallel walls at moderate {Reynolds} numbers},
booktitle = {{XVII Congresso di Meccanica Teorica ed Applicata}},
year = {2005}
}
@MISC{iCFDDatabase,
howpublished = {International CFD Database, http://cfd.cineca.it/},
key = {International CFD Database},
url = {http://cfd.cineca.it/}
}
@ARTICLE{vonfunck08a,
author = {W.~von~Funck and T.~Weinkauf and H.~Theisel and H.-P.~Seidel},
title = {Smoke Surfaces: An Interactive Flow Visualization Technique Inspired by Real-World Flow Experiments},
journal = {IEEE Transactions on Visualization and Computer Graphics (Proceedings Visualization 2008)},
year = {2008},
volume = {14},
pages = {1396--1403},
number = {6},
month = {November - December},
abstract = {Smoke rendering is a standard technique for flow visualization. Most
approaches are based on a volumetric, particle based, or image based
representation of the smoke. This paper introduces an alternative
representation of smoke structures: as semi-transparent streak surfaces.
In order to make streak surface integration fast enough for interactive
applications, we avoid expensive adaptive retriangulations by coupling
the opacity of the triangles to their shapes. This way, the surface
shows a smoke-like look even in rather turbulent areas. Furthermore,
we show modifications of the approach to mimic smoke nozzles, wool
tufts, and time surfaces. The technique is applied to a number of
test data sets.},
keywords = {Unsteady flow visualization, streak surfaces, smoke visualization},
url = {http://tinoweinkauf.net/}
}
Instead of or in addition to vonfunck08a, you may also cite this paper for visualizations and analysis results of this data set: