weinkauf/teaching/geometricmodeling14ss

Summer Semester 2014

• Saarland University
  Geometric Modeling
  Lecture with tutorials, 78476

• Instructors: Klaus Hildebrandt, Tino Weinkauf
• Tutors: Christian Schulz, Janick Martinez Esturo
• Semester: Summer 2014
• Lectures:
  • Mondays 12:15 - 13:45
    • Location: E1.4 Room 024 (MPII-Building)
  • Wednesdays 10:15 - 11:45
    • Location: E1.4 Room 021 (MPII-Building)
• Tutorials:
  • Fridays 12:15 - 13:45
    • Location: E1.4 Room 021 (MPII-Building)
• Credit Points: 9
• Office hours: Appointments can be coordinated via e-mail
• Class materials: Available for download. We tell you the username and password in the lecture. The lecture slides are available immediately after the lecture.

Announcements

July 15th: Summary lecture. You can ask any questions in preparation for the exam.

July 2nd: The lecture is cancelled.

May 12, May 19: Lectures take place in room 021 (not in 024).

The dates for the exam have been announced. See below.

May 5: You need to form groups of three students for the practical assignments. Follow the following algorithm:

• If you have already a group, send an email to Janick Martinez Esturo with the names of the members of your group.

• If you do not have a group, come to the programming tutorial on Monday, May 5th. We will form groups then.

  • If this does not work for you, send an email to Janick Martinez Esturo.

• We will determine the interview slots for the practical assignments and let you know via email. Conflicts will be figured out on an individual basis.

April 25: Register with us until Friday, April 25, by sending an email to Janick Martinez Esturo. Please send the following informations: Name, Studiengang, Matrikelnummer, EMail.

April 17: The first assignment is online. It deals with GeoX and some first examples using this software framework.

April 16: The lecture will start on Wednesday, April 16.

This page will be updated during the semester.

Overview

Recent progress in Geometric Modeling has been stimulated by numerous applications in engineering and multimedia. The purpose of the course is to give an introduction to classical and modern mathematical techniques employed in Geometric Modeling and to demonstrate how these techniques are useful for the design and manufacture of engineering objects of high quality, entertainment and multimedia applications. The course will also serve as a starting point for those students who wish to use Geometric Modeling concepts and ideas in their own research. Topics to be covered include shape interpolation and approximation with piecewise polynomial curves and surfaces, mesh processing, and multiresolution modeling.

Course topics:

• Mathematical background for geometric modeling

• Modeling Techniques:

  • Splines, curves and surfaces
  • Bezier splines, B-Splines, NURBS, implicits functions
  • Variational Modeling

• Geometry Processing:

  • Processing of 3D scanner data
  • Registration, reconstruction, data fitting

• Practical Skills:

  • Programming assignments & tutorials

Schedule

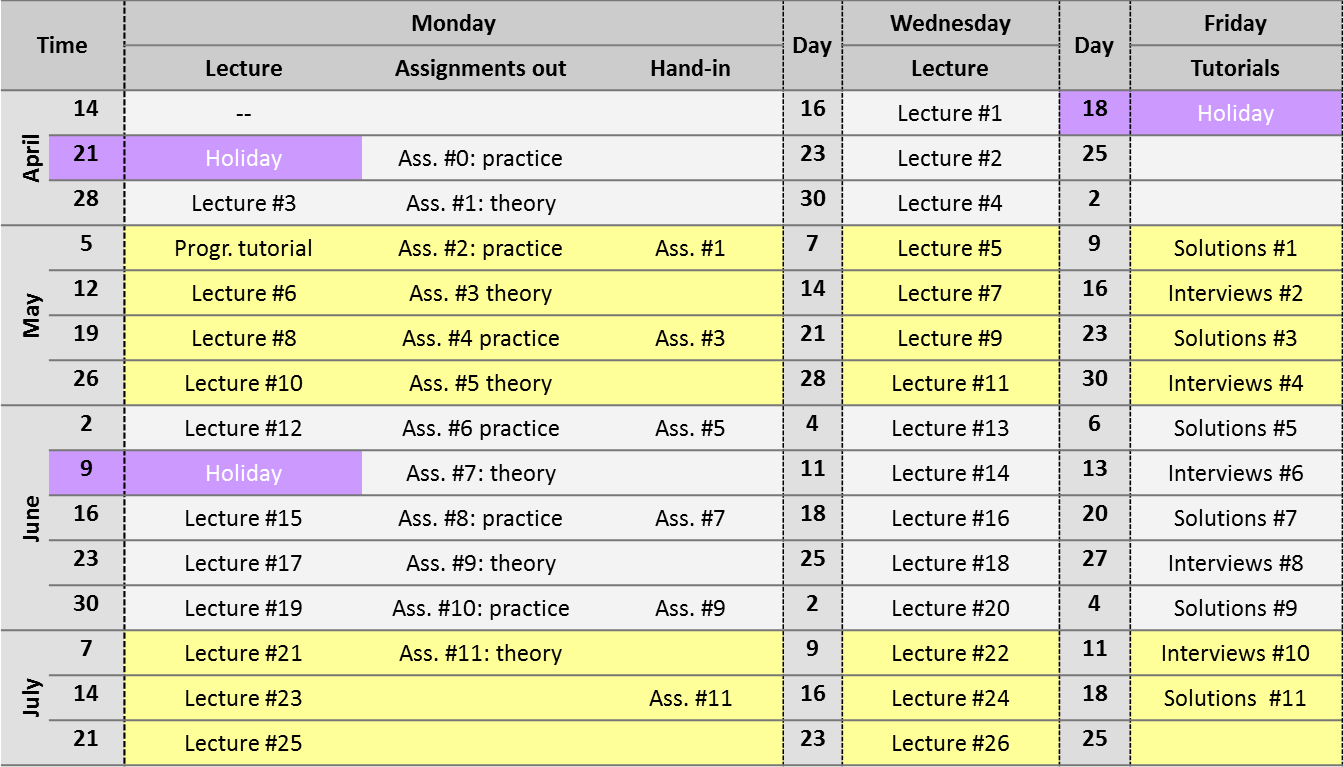
Schedule for the lectures and tutorials.

Software

GeoX is our programing framework for the practical tutorials. The software is open source (GPL2).

• Download the sources including an introduction to the GeoX framework

Expected Work

The course is suitable for MS students. Familiarity with basic computer graphics (or motivation to learn this fast) is desirable. Assessment is based on weekly assignments and a written exam at the end of the semester.

Literature

Main textbooks, on shelf in the CS-library ("Semesterapparat")

• Gerald Farin: Curves and Surfaces for Computer Aided Geometric Design (Fifth Edition), Morgan Kaufmann, 2002.
• Mario Botsch, Leif Kobbelt, Mark Pauly, Pierre Alliez, Bruno Levy: Polygon Mesh. Processing, AK Peters, 2010.
• Alfred Gray: Modern Differential Geometry of Curves and Surfaces with Mathematica (Second Edition), CRC, 1997.
• Wolfgang Kühnel: Differential Geometry: Curves - Surfaces - Manifolds, American Mathematical Society, 2005.
• Additional textbooks on shelf in the CS-library

Recommended additional reads:

• Richard O. Duda, Peter E. Hart, David G. Stork: Pattern Classification (Second Edition), Wiley & Sons, 2000.

  • Relevant Topics: Statistical techniques, least-squares, total-least-squares (PCA)

• James D. Foley, Andries VanDam und Steven K. Feiner: Computer Graphics: Principles and Practice, Addison-Wesley, 1992.

  • Relevant Topics: Computer Graphcis, Fourier Transform & Signal Theory (Chapter 14.10).

Try out this:

• CAGD applets from the Geometric Design Group of the University of Karlsruhe