Alper Aydemir

Understanding indoor environments

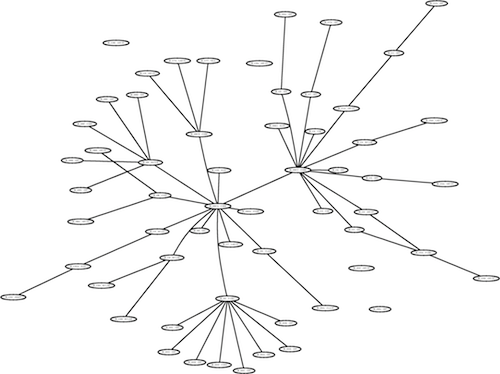
Here's a visualization of a topological map of a building from the dataset. The edges represent navigability between the rooms. Hover over nodes to see categories:

Instructions to download the dataset, libfloorplan and the annotation tool

Click here to download the KTH dataset. For the MIT dataset, please send an email to Prof. Teller with me Cc'ed so I can send the download link to the MIT dataset upon his approval.

Click here to download the libfloorplan C++ library. It provides the necessary code to parse the XML files and more. Any additional features, bug fixes are most welcome. Feel free to contact me if you face any problems. Click here to download the Qt based annotation tool. You can annotate images of floorplans using this tool and help extend the dataset.

For the KTH dataset, please cite the below reference for any publications that makes use of the dataset.

@inproceedings{aydemir2012,
title = {What can we learn from 38,000 rooms? Reasoning about unexplored space in indoor environments},
author = {Alper Aydemir, Patric Jensfelt and John Folkesson},
booktitle = {2012 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS)},
year = {2012},
organization = {IEEE}
}

For the MIT dataset, please cite the below reference for any publications that makes use of the dataset.

@inproceedings{whiting2007,
title = {Generating a Topological Model of Multi-Building Environments from Floorplans},
author = {Emily Whiting, Jonathan Battat, and Seth Teller},
booktitle = {CAAD (Computer-Aided Architectural Design) Futures 2007},
year = {2007},
month={July},
pages={115-28},
address={Sydney,Australia}
}

Robots that can handle the spatial complexity of man-made indoor environments is a long term of robotics research. We analyze buildings of the KTH and MIT campuses. In total this amounts to nearly 38,000 real-world rooms. Each room in the dataset has its 2D layout and category (office, corridor, kitchen etc.).

Building on this rich data, we extract certain statistics to perform predictions in large floorplan datasets.

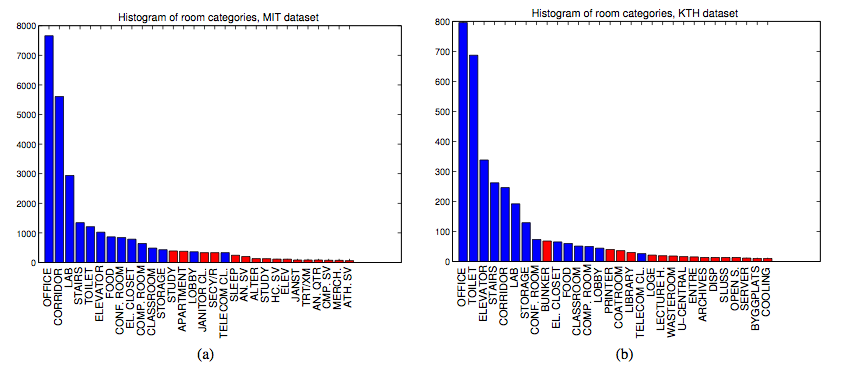
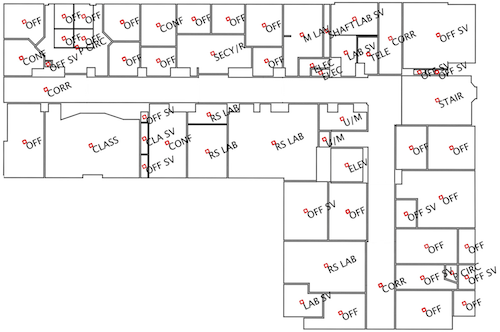
Shown here are the 2D layout of one of the floors and it's topological map equivalent. Specifically, using tools from graph theory, we first analyze certain characteristics indoor topologies such as scale-freeness, cluster coefficient, characteristic path length .

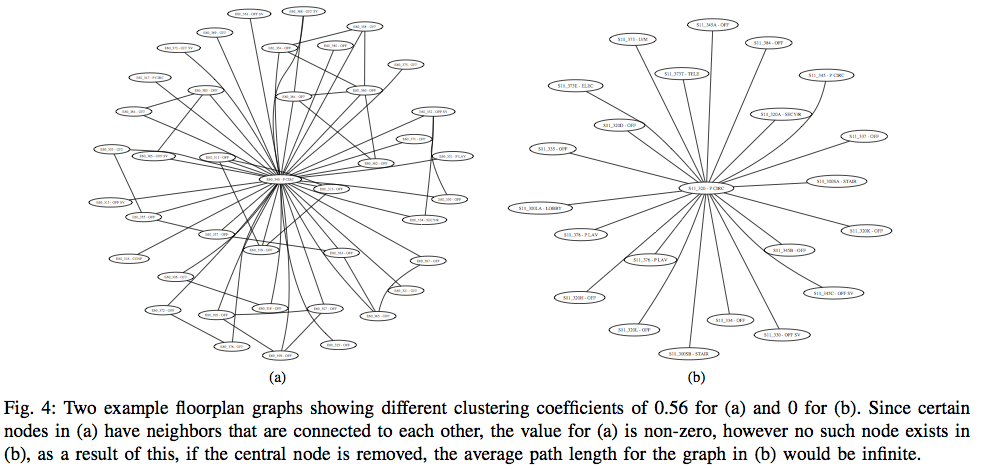
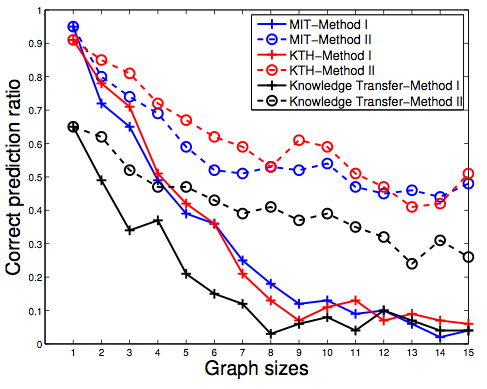
Following this analysis, we propose two methods for predicting both the topology and the categories of rooms given a partial map. We provide extensive experimental results that evaluate their performance. In particular, we analyze the transferability of our models between the two data sets. We also provide the KTH data set and the software tool publicly available.

Our results indicate that the proposed methods are able to capture the structure of indoor topologies. We believe with this study we have only scratched the surface of analyzing man-made environments on the very large scale.