Florian T. Pokorny
Assistant Professor, School of Computer Science and Communication, KTH Royal Institute of TechnologySelected Work on Robotic Grasping and Manipulation
Topological Ideas for Grasp Synthesis
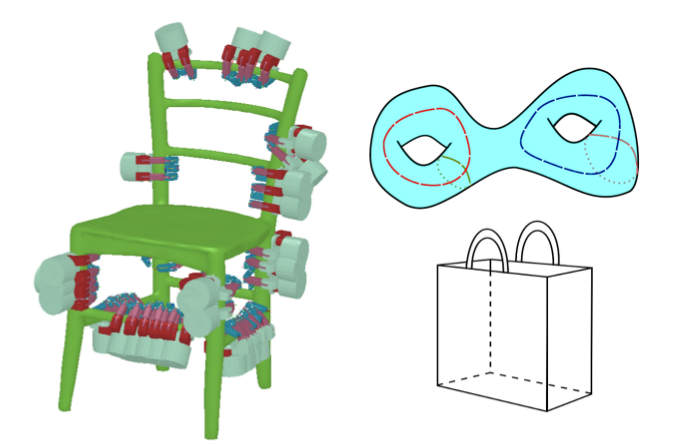
I am interested in novel topologically motivated representations that can be used for robotic grasping. In our recent
work "Grasping Objects with Holes: A Topological
Approach" (ICRA 2013, with J. A. Stork, D. Kragic), we investigate using topological features of an object with
holes. For this purpose, we make use of the first homology group $H_1(X)$ of a surface $X\subset \mathbb{R}^3$.
$H_1(X)$, when computed with coefficients in a field, is a vector space whose non-zero elements correspond to
equivalence classes of non-contractible
loops on $X$. Our work introduces these topological notions for grasping. We adapt ideas coming from the Gauss linking
integral and the notion of winding numbers in topology to define a simple controller leading a robotic hand to securely
clasp around such loops. Recently, we combined this approach with motion planning and introduced a notion of virtual
linking. Our paper A Topology-based Object Representation for
Clasping, Latching and Hooking" (Humanoids 2013, J. A. Stork, F. T. Pokorny, D. Kragic) has been selected as runner-up for the best conference award at Humanoids
2013.
Our work in Danica Kragic's lab is partially funded by the EU
FP7 project TOMSY which investigates topological techniques for dexterous manipulation.

Grasp Moduli Spaces and Continuous Representations
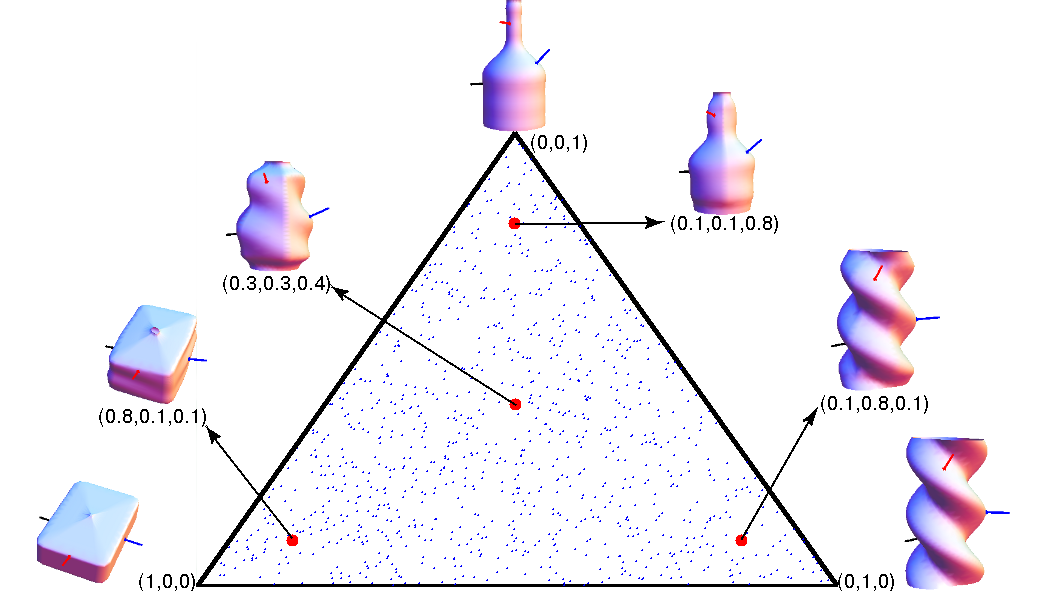
Our recent work "Grasp Moduli Spaces" (RSS 2013, with K.
Hang, D. Kragic) is part of our efforts to introduce new continuous parametrizations to robotics which are capable of
describing shapes and grasps in a single space. Based on such spaces we are interested in developing deformation based
approaches to manipulation which are capable to transfer grasps across similar object instances.

Grasp Quality Functions
Grasp synthesis algorithms commonly use grasp quality assessment functions which measure how physically stable or
suitable a grasp is. In our work
Classical Grasp Quality Evaluation: New Theory and
Algorithms (IROS 2013, with D.Kragic), we investigate new efficient methods for computing
a popular grasp quality measure introduced by Ferrari and Canny. The computation of this grasp quality measure
classically relies on an approximation of friction cones by polyhedral cones. We make precise error bounds when
applying this approach and prove that the underlying grasp quality measure $Q$ is in fact Lipschitz continuous
with a particular Lipschitz constant. This implies a novel analytic bound on the variability of grasp quality
around any given grasp which is useful in the presence of noise, or when a deformation based grasp synthesis approach is
to be considered. Another aspect of grasp evaluation I am interested in is the development of task specific grasp
quality measures.