Florian T. Pokorny
Assistant Professor, School of Computer Science and Communication, KTH Royal Institute of TechnologyComputational Geometry and Machine Learning methods for Robotics and Data Analytics
I am working on methods that generate high-quality configuration space models from sampled point-cloud data. In our recent work at Robotics: Science and Systems, 2014, "Multiscale Topological Motion Classification with Persistent Homology", we applied filtrations of simplicial complexes for the first time as a tool to model robot configuration spaces. Using persistent homology (see e.g. Gunnar Carlsson's group at Stanford), this enabled us to classify trajectories topologically, rather than geometrically, thus allowing a robot to reason at a topological abstraction layer about the space of trajectories. An IJRR journal version of this paper is currently under preparation.
Topological Methods for Machine Learning
I am interested in the use of persistent homology for machine learning applications. In our work "Persistent Homology for Learning Densities with Bounded Support" (NIPS 2012, with C.H. Ek, H. Kjellström, D. Kragic), we investigate how prior knowledge on the topological structure of the support region $\Omega$ of a probability density $f:\mathbb{R}^d \mapsto \mathbb{R}$ can be used to improve the quality of a kernel based density estimator of the form $$\hat{f}_{\epsilon, n}(x) = \frac{1}{\epsilon n^d}\sum_{i=1}^n K\left(\frac{x-X_i}{\epsilon}\right).$$ We show the convergence of our estimator in experiments and demonstrate that our ideas can be used to reliably model trajectories of a race-car going around a track.
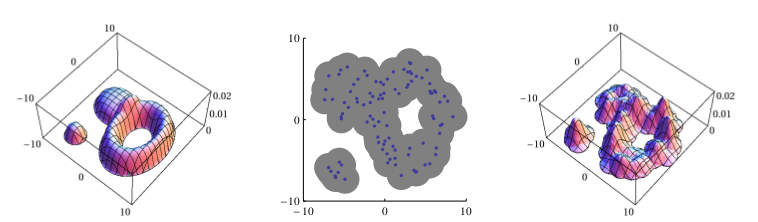
Original density (left), random samples (centre) and kernel based density estimator (right) which correctly
recovers the `hole' and the number of connected components of the support region.
Previous work: Toric Kähler Geometry
This work concerns the properties of the Bergman kernel on toric Kähler manifolds. Kähler manifolds are special types of manifolds with a Riemannian, symplectic and holomorphic structure
which are mutually compatible in a beautiful way. During my PhD, I studied in particular polarized toric Kähler manifolds which are linked to the combinatorics of polytopes and which are
additionally projective algebraic varieties. Such polarized Kähler manifolds $(X, \omega)$ come with a sequence of holomorphic Hermitian line bundles $(L^k, h)$, for $k\in \mathbb{N}$. The Bergman kernel $B_k$ then represents
the orthogonal projection from smooth to holomorphic sections of these line bundles. In my thesis "The Bergman Kernel on Toric Kähler manifolds",
I studied this projection and a generalization of it which results in a partial Bergman kernel. I was able to obtain some asymptotic coefficients of the diagonal of these kernels as the power $k$ of the line bundle $L^k$ is increased. These coefficients link the algebraic structure of $X$ to the geometry. An extension of my thesis work
"Toric partial density functions and stability of toric varieties"
(with M.Singer) has recently been accepted for publication at Mathematische Annalen.
Here is a conference video of my presentation of some results on Toric Kähler manifolds (with Michael Singer), presented at Cambridge University.