Florian T. Pokorny
Assistant Professor, School of Computer Science and Communication, KTH Royal Institute of TechnologyHarmonicRegression (C++/Python)
This C++ library with python bindings implements spherical harmonics and an associated least-squares regression to recover a smooth surface description from point-cloud data. These methods are described in our paper"Grasp Moduli Spaces and Spherical Harmonics", F. T. Pokorny, Y. Bekiroglu, D. Kragic, IEEE ICRA, 2014
This software is freely available for academic/research purposes, just drop me an email to get the code: fpokorny (at) kth.se
Introduction
Consider the space $L^2(\mathbb{S}^2)$ of integrable functions on the sphere $\mathbb{S}^2\subset \mathbb{R}^3$. We choose a coordinate chart $p(\theta, \phi) = (\sin \theta \cos \phi, \sin \theta \sin \phi, \cos\theta)$ on the sphere, with $(\theta, \phi) \in [0, \pi]\times [0, 2\pi)$. For integers $l, m$, the real valued spherical harmonic function of degree $l$ and order $m$, $|m|\le l$, is defined by \[ Y_{l,m}(\theta, \phi) = \begin{cases} c_{l,m}P_l^{|m|}(\cos \theta)\sin (|m|\phi) & -l\le m \le -1\\ \frac{c_{l,m}}{\sqrt{2}}P_l^0(\cos \theta) & m = 0\\ c_{l,m}P_l^{m}(\cos \theta)\cos(m\phi) & 1\le m \le l, \end{cases} \] where $c_{l,m} = \sqrt{\frac{2l+1}{2\pi}\frac{(l-|m|)!}{(l+|m|)!}}$ and $P_l^m$ denotes the associated Legendre polynomial of order $m$ and degree $l$. The functions $Y_{l,m}$ arise as eigen-functions of the Laplacian $\Delta=\frac{1}{\sin\theta}\frac{\partial}{\partial\theta}(\sin\theta \frac{\partial}{\partial\theta})+\frac{1}{\sin^2\theta}\frac{\partial^2}{\partial^2\phi}$ on $\mathbb{S}^2$ For fixed $l$, there are $2l+1$ eigenfunctions $\{Y_{l,m}: m\in\{-l, \ldots, l\}\}$ satisfying \[ \Delta Y_{l,m} = \lambda_l Y_{l,m}, \] where $\lambda_l = l(l+1)$ denotes the corresponding eigen-value. These eigen-functions, for all $l, m$, form an infinite orthonormal basis for $L^2(\mathbb{S}^2)$ with respect to the standard inner product $\langle f, g\rangle = \int_{\mathbb{S}^2} fg \,dVol$, for $f, g\in L^2(\mathbb{S}^2)$ and where $dVol = \sin \theta d \theta d \phi$.
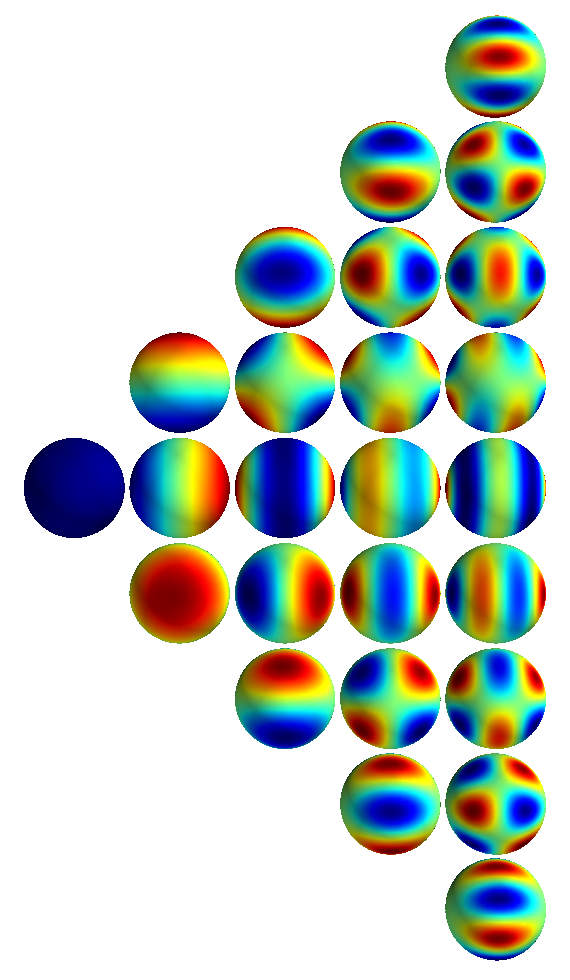
A visualization of the functions $Y_{l, m}$, where the degree changes from 0 to 4 along the horizontal axis
and the order $m$ changes from $-l$ to $l$ along the vertical axis.
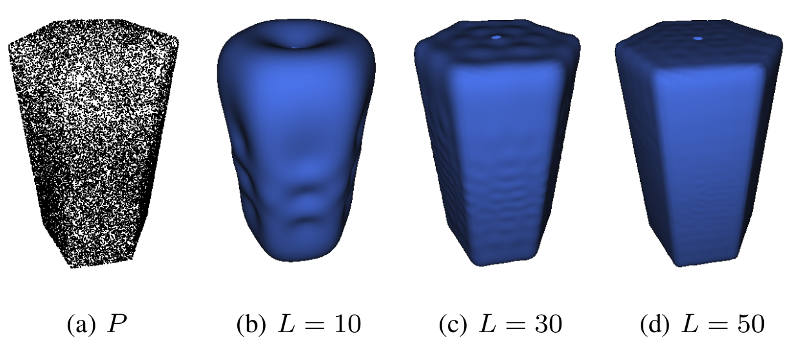
Point cloud P with 25000 points and reconstructed surfaces, where all eigen-spaces up to degree $L$ are used.