This data set contains 100000 random grasp point-contact configurations formed by uniformly sampled contact points
and unit surface normals as well as associated centres of mass. These contact configurations are useful for large scale
statistical studies of grasp quality measures but do not necessarily correspond to specific object/hand configurations.
Associated grasp quality scores are available for download for further analysis.
See the following papers for use cases:
"Classical Grasp Quality Evaluation: New Theory and Algorithms", F. T. Pokorny, D. Kragic, IEEE/RSJ IROS, 2013
"Friction Coefficients and Grasp Synthesis", K. Hang, F. T. Pokorny, D. Kragic, IEEE/RSJ IROS, 2013
"Grasp Moduli Spaces", F. T. Pokorny, K. Hang, D. Kragic, RSS 2013.
This data is freely available for academic/research purposes, just drop me
an email to get it:
fpokorny (at) kth.se.
Introduction
Here is a snapshot of two grasps in the data-set. Have a look at the tutorial
for the
FastGrasp library to download the python
scripts to work with this data.
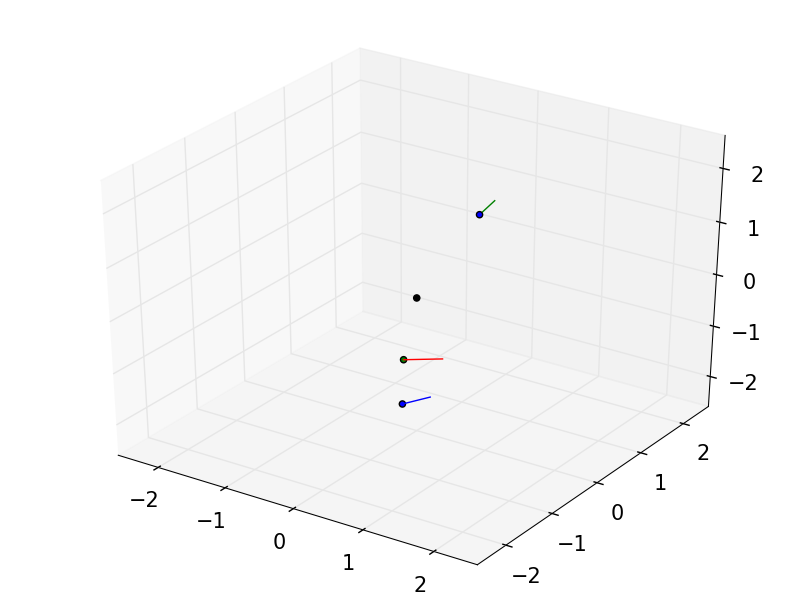
An unstable grasp
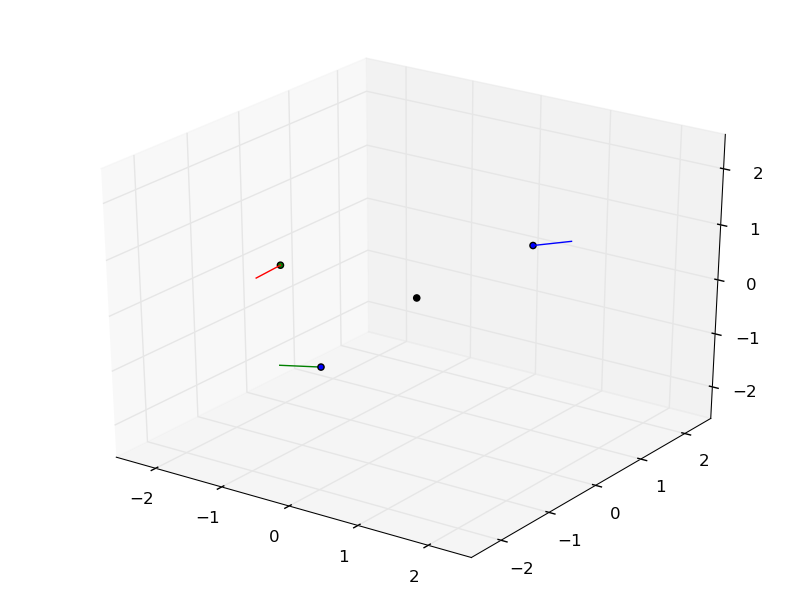
A stable grasp
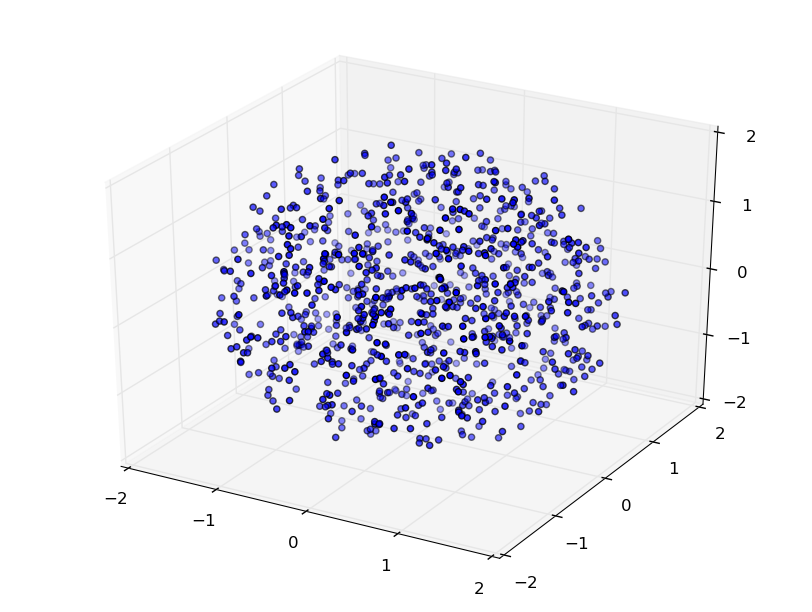
The positions of contact 1 for the first 1000 grasps
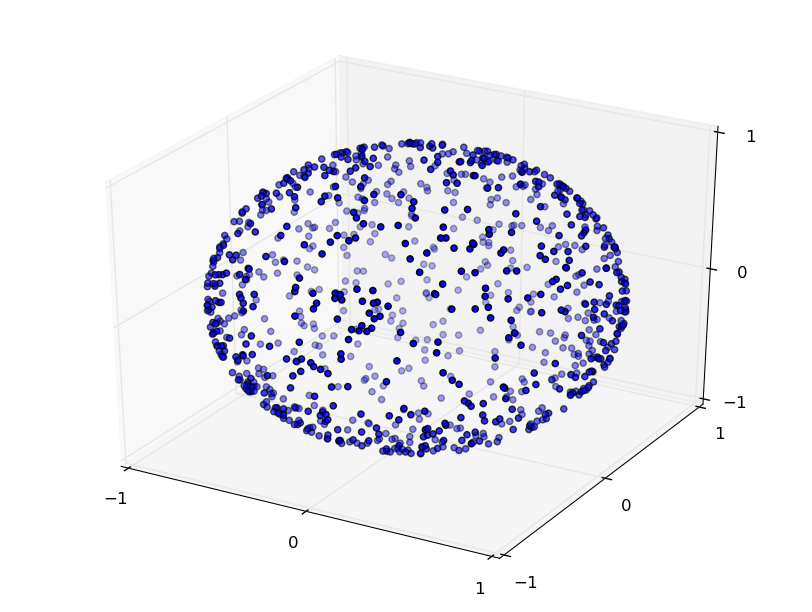
The normals of contact 1 for the first 1000 grasps
Files
grasps100k.npy
A numpy matrix which stores one grasp per row and 100000 grasps in total.
Each row is of dimension 21. The first 3 columns are the coordinates of the
first grasp contact, then follow the 3D coordinates of contact 2, 3, then
of the 3 inward pointing unit normal vectors, normal to hypothetical surface parts
containing the 3 contacts. Finally, a centre of mass of the hypothetical surface
is provided. This is always zero in this grasp set.
All grasps lie in the set $\mathcal{D}(2) = \mathbb{B}(2)^3 \times (\mathbb{S}^2)^3 \times \{0\}$, where $\mathbb{B}(2)
= \{x\in \mathbb{R}^3: |x|\le 2\}$. All contacts hence have distance at most 2 from the centre of mass (= the origin).
The grasps are sampled uniformly in the sense that contact points are sampled from the uniform distribution on the
ball $\mathbb{B}(2)$ and unit normals are sampled using the uniform distribution on the 2-sphere $\mathbb{S}^2\subset\mathbb{R}^3$.
grasps100k_qhull.npy
A numpy matrix with $Q_l^-$ grasp quality lower-bound evaluations for each grasp
in
grasps100k.npy. Columns 1-19 are corresponding to $l=3,4,\ldots,20$ edges per
friction cone approximation and column 20 stores the values of $Q_{40}^-$ obtained
using a previous implementation of $Q_l^-$ similar to the one provided in
FastGrasp.
In all computations, we used a friction coefficient of 1.
Note that the computation of $Q_{40}^-$ takes significant computational time (several hours)
for the full set of 100000 grasps.
grasps_qhull_times.npy
A numpy matrix with computation times for $Q_l^-.$ Here, consider $U_1, \ldots, U_{10}$
to be a splitting of the grasps in
grasps100k.npy into 10 consecutive sets of 10000 grasps each.
the $i^{th}$ row of
grasps_qhull_times.npy gives the wall timings in seconds for the computation of
the $Q_l^-$ values for $l=3,4,...,20,40$ for a previous implementation of $Q_l^-$ similar to the one
provided in
FastGrasp. In all computations, we used a friction coefficient of
1.
grasps100k_unstable.npy
A grasp set analogous to
grasps100k.npy. However, here grasps were sampled using rejection
sampling and only grasps which satisfied $Q_{20}^-(g) = 0$ were added to the data-set. The vast
majority of grasps in this data-set are hence unstable also with respect to the analytic
$Q(g)$ grasp quality. This data-set is used to test our unstable grasp rejection algorithm.
In all computations, we used a friction coefficient of 1.
grasps100k_upper.npy
A numpy matrix with one row per grasp in
grasps100k.npy. Each row stores the results of
a version of Algorithm 2 in
"Classical Grasp Quality Evaluation: New Theory and Algorithms"
which can be used to determine an upper bound to the grasp quality $Q$. Each row stores the
final $q^+$ value of that Algorithm (see paper) and $N = 1000$ iterations and $M\in \{1, 5, 10,
20, 30, 40, 50\}$ random samples (see paper). Note that $\max(0, q^+(g))$ yields an upper bound
for $Q(g)$. In all computations, we used a friction coefficient of 1.
grasps100k_upper_times.npy
A numpy matrix storing the wall times for the computation leading to
grasps100k_upper.npy.
The $i^{th}$ row records computation times for grasp $10000i$ to $10000(i+1)-1$.
Each row has 7 entries corresponding to the parameter setting $M \in \{1, 5, 10, 20, 30, 40, 50\}$.
In all computations, we used a friction coefficient of 1.



