Documentation Contents:
- Introduction
- Tutorial
- Installation Instructions
Introduction
This library is concerned with the evaluation of a classical $L^1$ grasp quality score $Q(g)$ for a grasp contact
configuration $g$ which was originally defined by Ferrari and Canny. The value of $Q(g)$ is defined to be the radius of
the largest ball around the origin completely contained in the grasp wrench space $W$, if such a ball exists and $0$
otherwise. This value cannot be computed precisely and a typical approach has hence been to approximate $W$ by a smaller
convex hull spanned by finitely many points and which is obtained by approximating the friction cone $F$ at each contact by
convex polyhedral cones $F_l$ with $l$ edges.
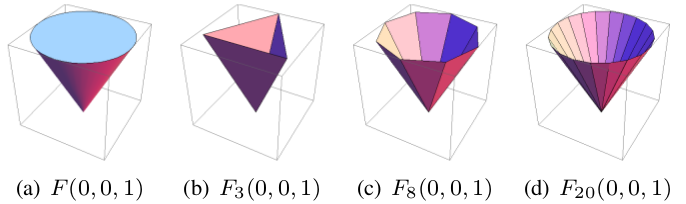
Polyhedral cone approximations of a friction cone
The resulting grasp quality approximation $Q_l^-(g)\le Q(g)$ has been popular in the grasping community for more than a
decade. Our paper
"Classical Grasp Quality Evaluation: New Theory and Algorithms", F. T. Pokorny, D. Kragic, IEEE/RSJ IROS, 2013
establishes for the first time error bounds on this approximation and provides a novel approach
to also obtain an upper bound $Q^+(g)$ so that
$$Q_l^-(g)\le Q(g) \le Q^+(g).$$
This library provides functions to compute $Q_l^-(g)$ and $Q^+(g)$. We use a subgradient-based method to compute $Q^+(g)$
as outlined in the above
paper.
Additionally, we provide a novel algorithm to speed-up the computation of $Q_l^-(g)$ by first filtering out unstable
grasps using a convex optimization procedure. This results
in a significant speedup compared to a standard evaluation of $Q_l^-(g)$.
Tutorial
Once you have followed the
installation instructions,
make sure you have the interactive python console (IPython) installed and go to the folder
./python/src
and start an interactive python session (ipython). Try the following:
import numpy as np
import PyFastGrasp
grasps = np.load('../../data/random_grasps/grasps100k.npy')
The numpy matrix stores one grasp per row and 100000 grasps in total.
Each row is of dimension 21. The first 3 columns are the coordinates of the
first grasp contact, then follow the 3D coordinates of contact 2, 3, then
of the 3 inward pointing unit normal vectors, normal to hypothetical object parts
containing the 3 contacts. Finally a centre of mass of the hypothetical object
is provided. This is always zero in this grasp set.
All grasps lie in the set $\mathcal{D}(2) = \mathbb{B}(2)^3 \times (\mathbb{S}^2)^3 \times \{0\}$, where
$\mathbb{B}(2)=\{x\in \mathbb{R}^3: |x| \le 2\}$. Hence, all contacts have distance at most 2.0 from the centre of mass
(= the origin). The grasps are sampled uniformly in the sense that contact points are sampled from the uniform
distribution on $\mathbb{B}(2)$ and unit normals are sampled using the uniform distribution on the 2-sphere $\mathbb{S}^2$ in
$\mathbb{R}^3$.
To get a better idea of these grasps, run
in the ipython console. This will display the first 1000 contact configurations and normals as shown below:
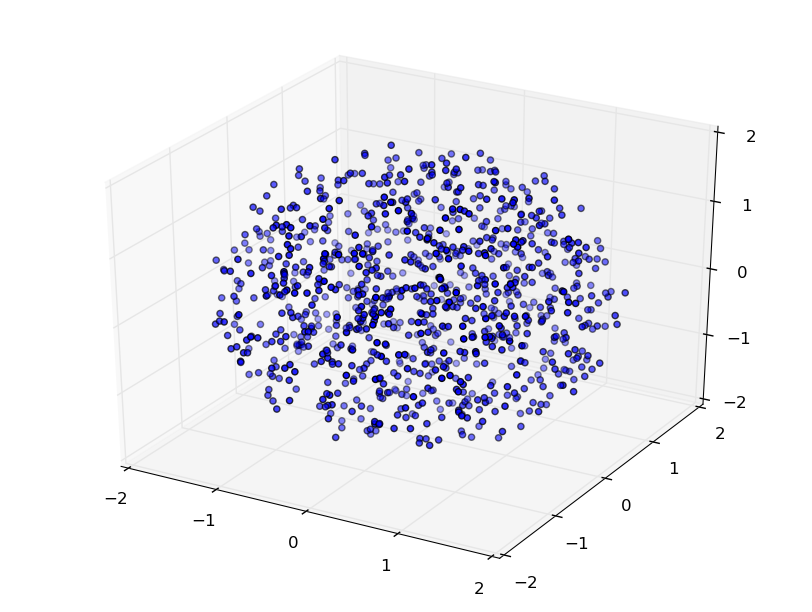
The positions of contact 1 for the first 1000 grasps
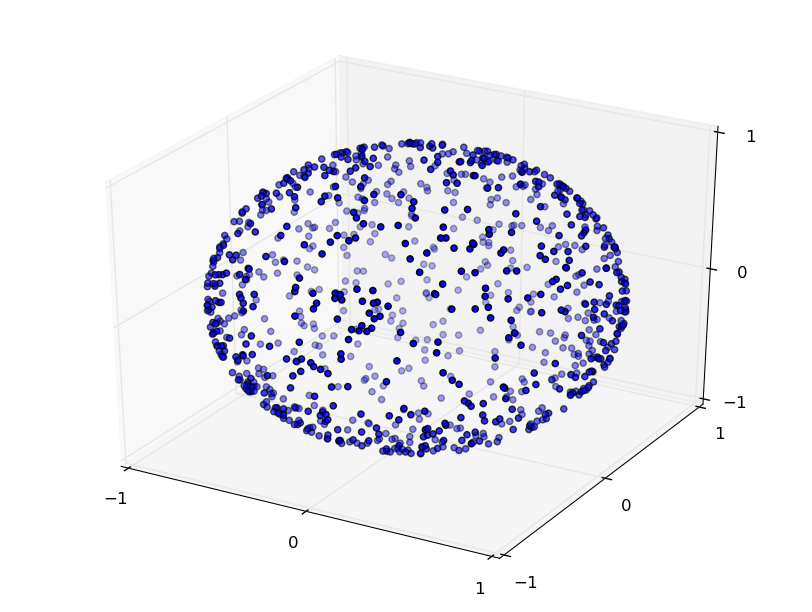
The normals of contact 1 for the first 1000 grasps
Furthermore, the script will display two examples of grasps as follows:
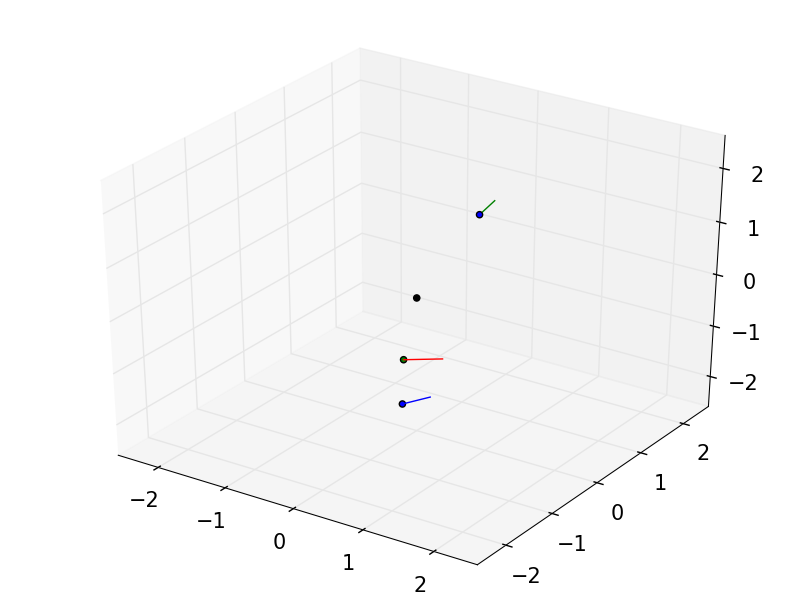
An unstable grasp
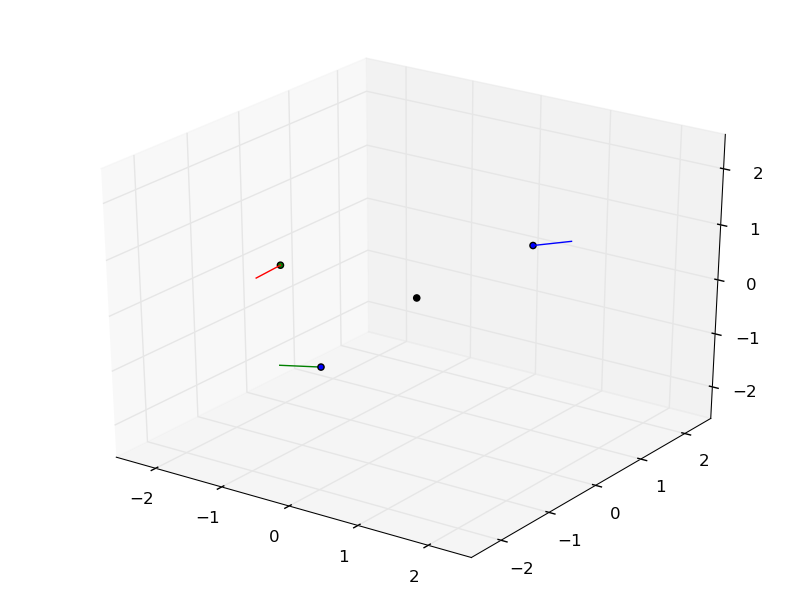
A stable grasp
The black dot indicates the centre of mass, and surface normals are indicated by thin lines emanating from
each of the three contact points.
To see the convergence of upper and lower bound estimates presented in our
paper,
you can run:
%run ./ComputeBounds.py
# the following variables are of interest: lowerBounds, upperBounds
print lowerBounds.max()
print upperBounds.max()
You will see the following plots, similar to the ones presented in the
paper:
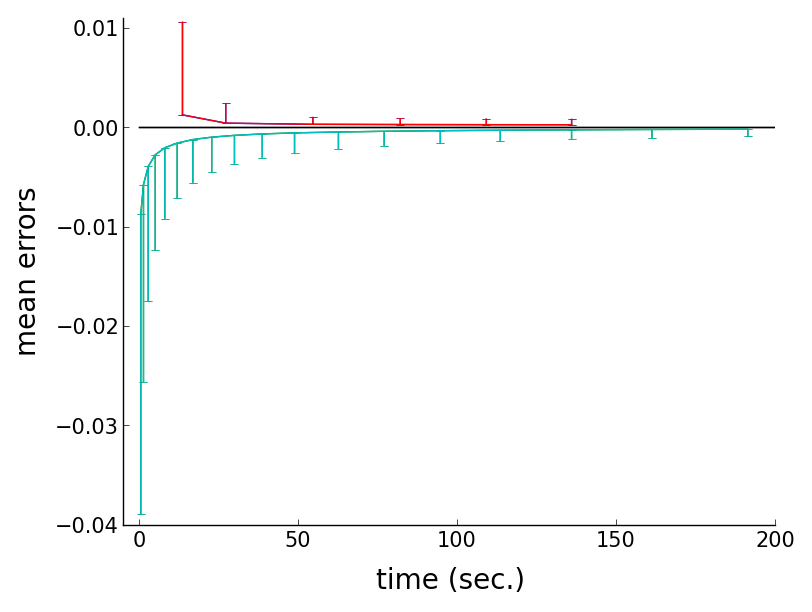
Convergence of upper/lower bound mean errors
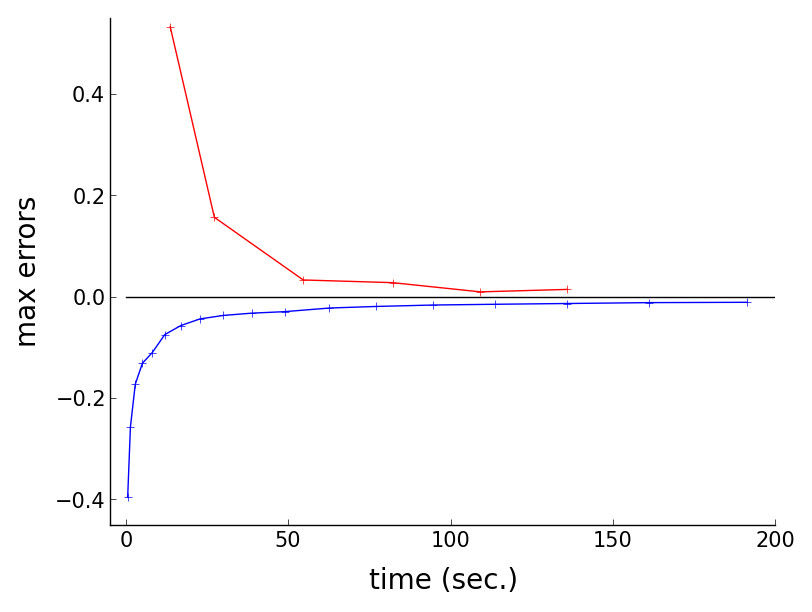
Convergence of upper/lower bound max errors
You can change the
mode variable to run computations on subsets of the grasps.
The script
UnstableRejection.py in turn uses our unstable grasp rejection algorithm
which relies on convex optimization to determine unstable grasps very quickly.
It can classify thousands of unstable grasps in a few milliseconds.
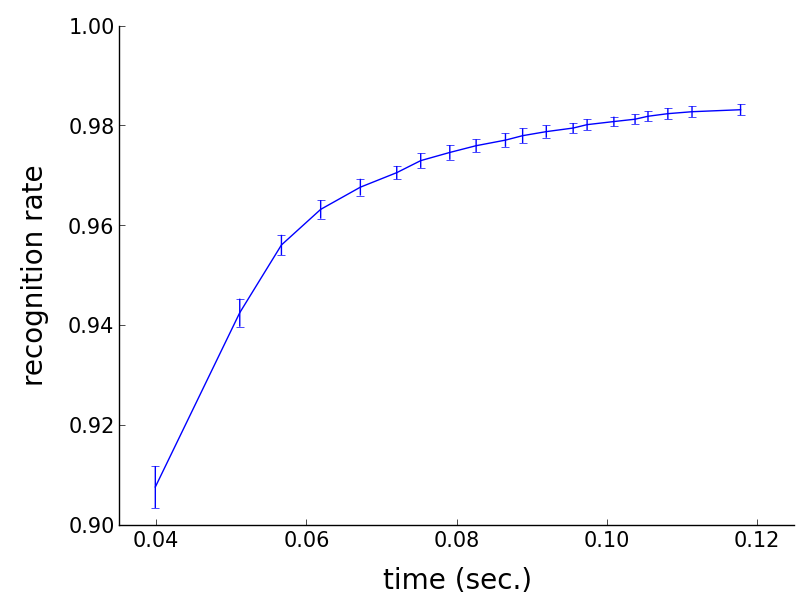
Recognition of unstable grasps
Based on this rejection algorithm, we can efficiently evaluate lower bounds by first removing the vast
majority of unstable grasps (with grasp quality 0.0). This idea is used in the script
PurgeGrasps.py.
Installation Instructions
You can obtain the source-code for this library by dropping me an email at
fpokorny
(at) kth.se. Make sure you have installed the SWIG, Eigen and Boost C++ libraries and the QHull C library. The compilation has so
far only been tested on Linux.
Unzip the file
FastGrasp.0.1.zip and run the
following in a terminal:
cd ./FastGrasp
./setup.sh
This will compile the library and generate a python interface.
Uou can use the executable in
./cpp/build/grasp_tool to run some basic experiments on grasp data.
A more convenient option is the use of the python library which is provided. In order to run the example code,
download the
RandomGrasps data set and store these files in
./data/random_grasps.







