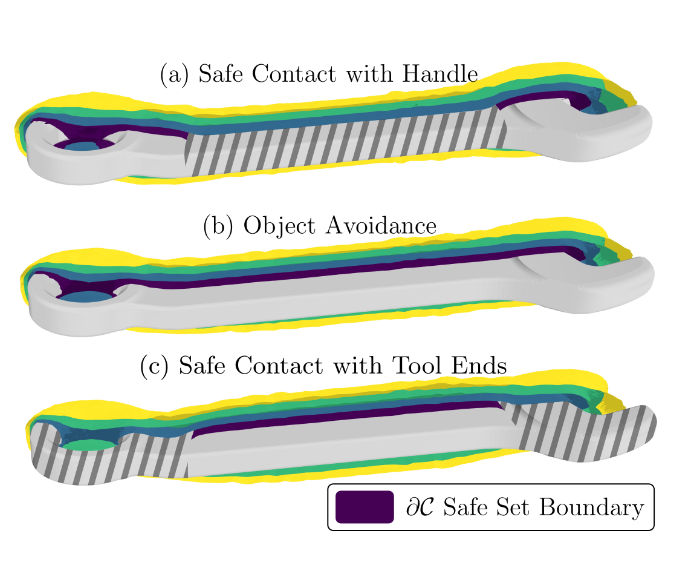
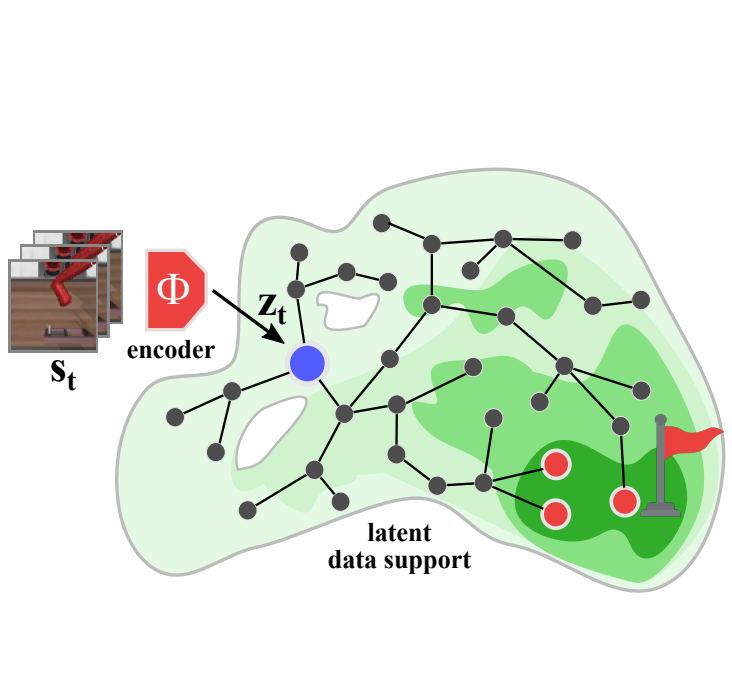
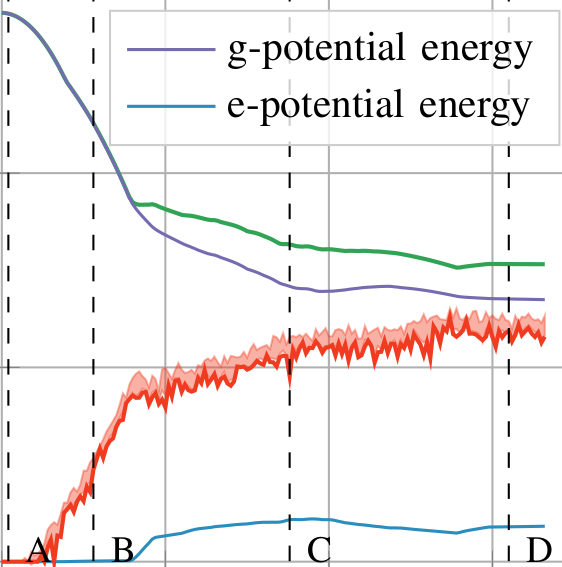
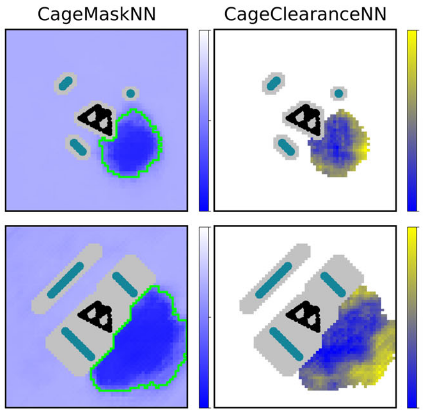
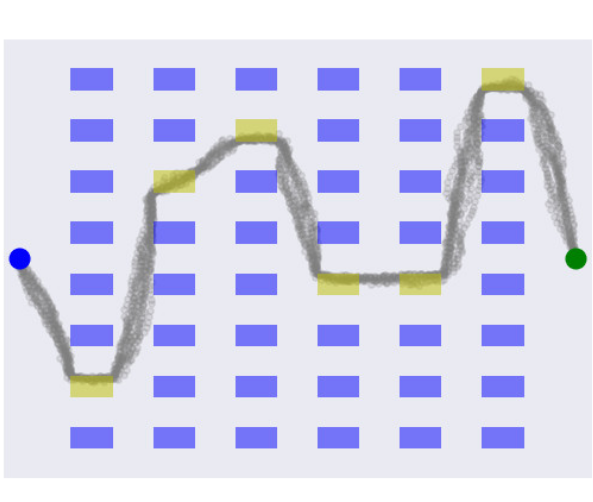
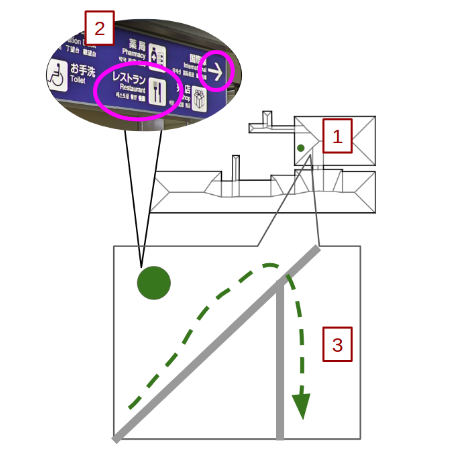
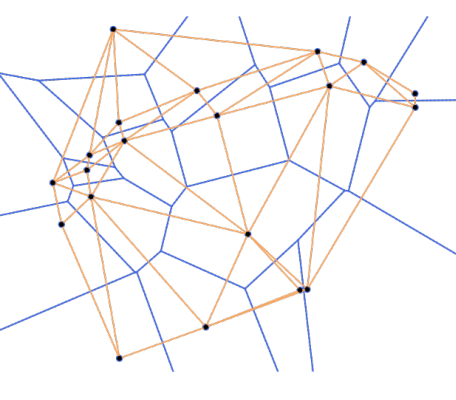
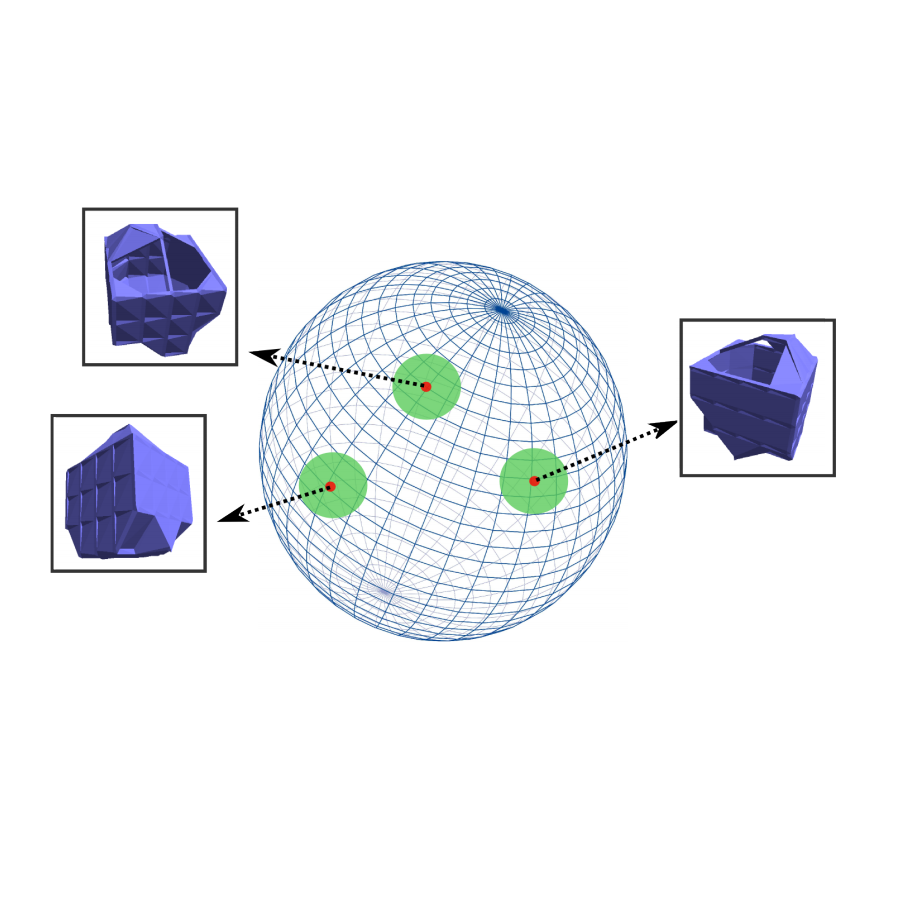
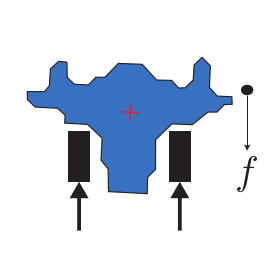
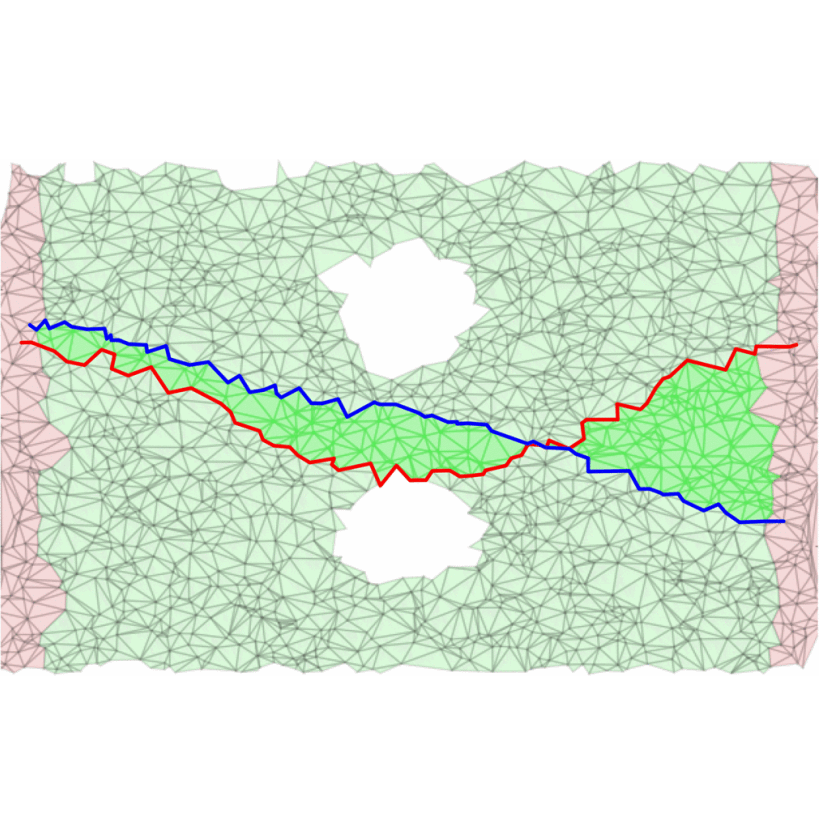
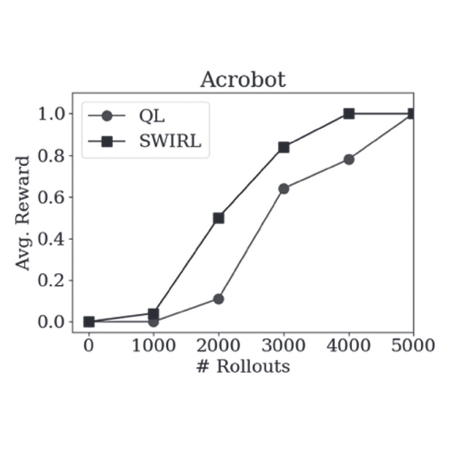
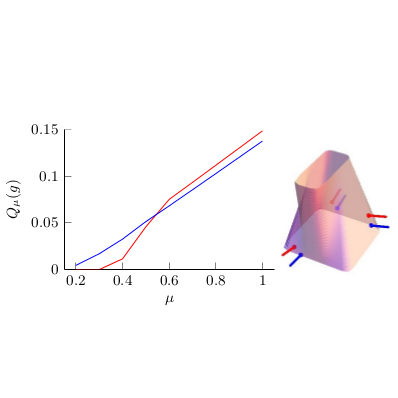
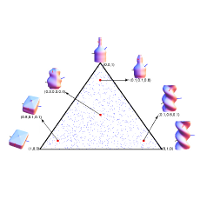
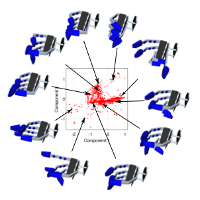
Welcome
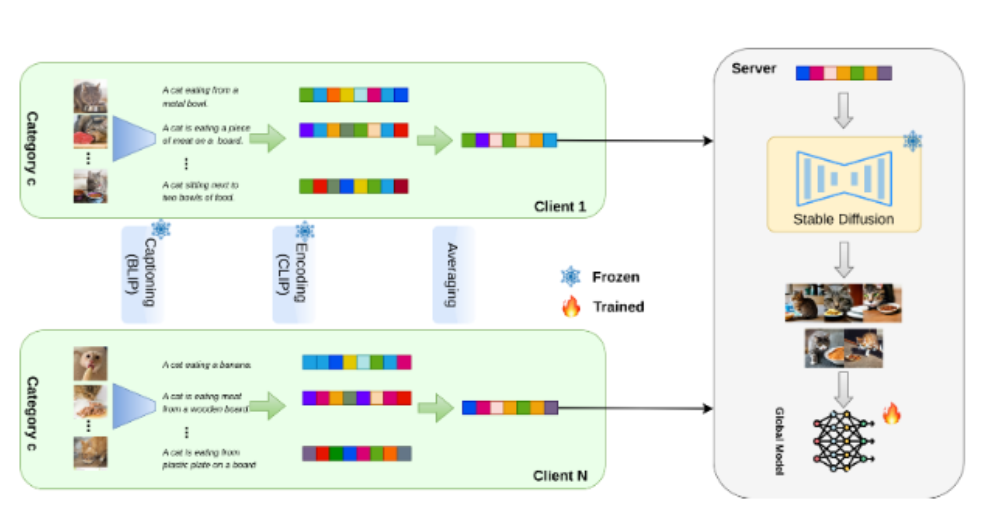
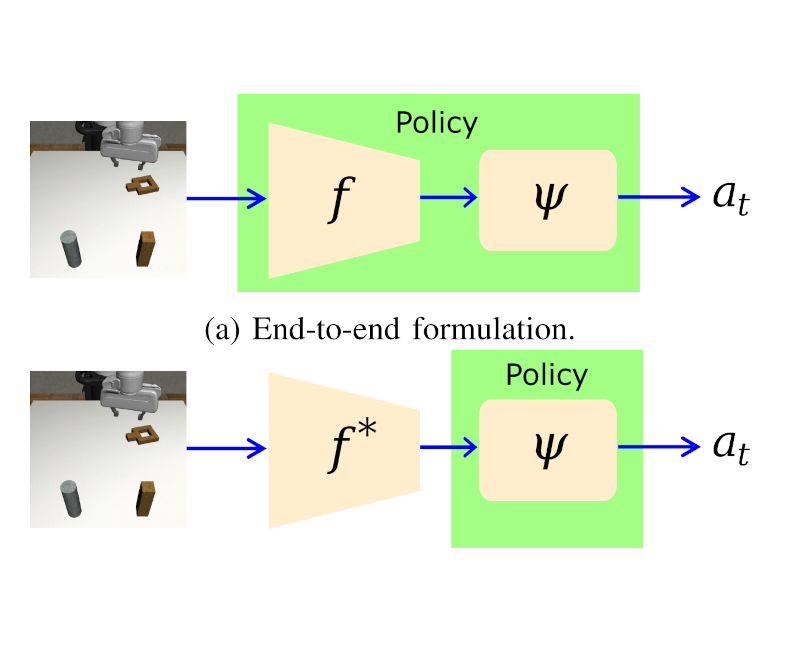
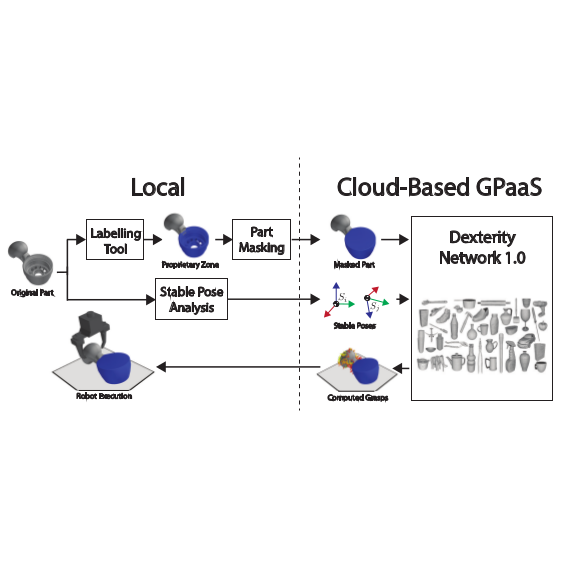
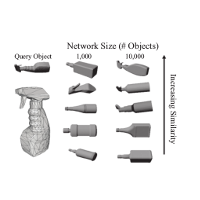
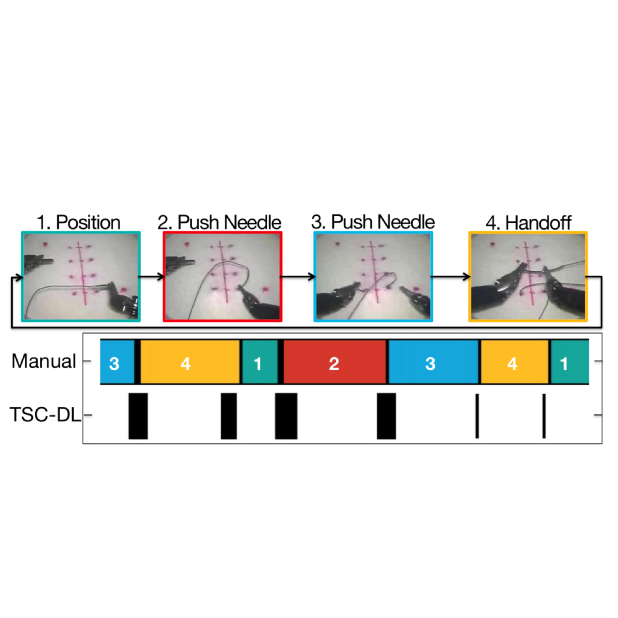
My group's research focusses on data-driven methods for robotic manipulation. Our recent interests include the understanding of training
data requirements and transfer learning for training machine learning methods for robotic manipulation at scale and challenges in
applying cloud robotics as a paradigm for robotic manipulation. Our work
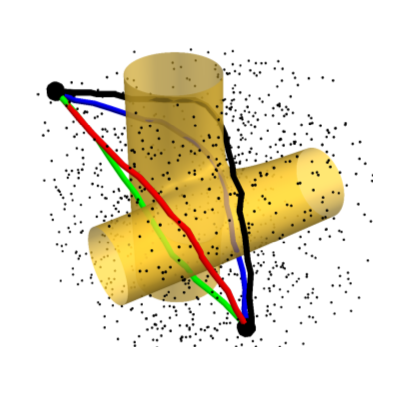
utilizes both state of the art deep learning and data-driven geometric and topological methods for reasoning about robot-object
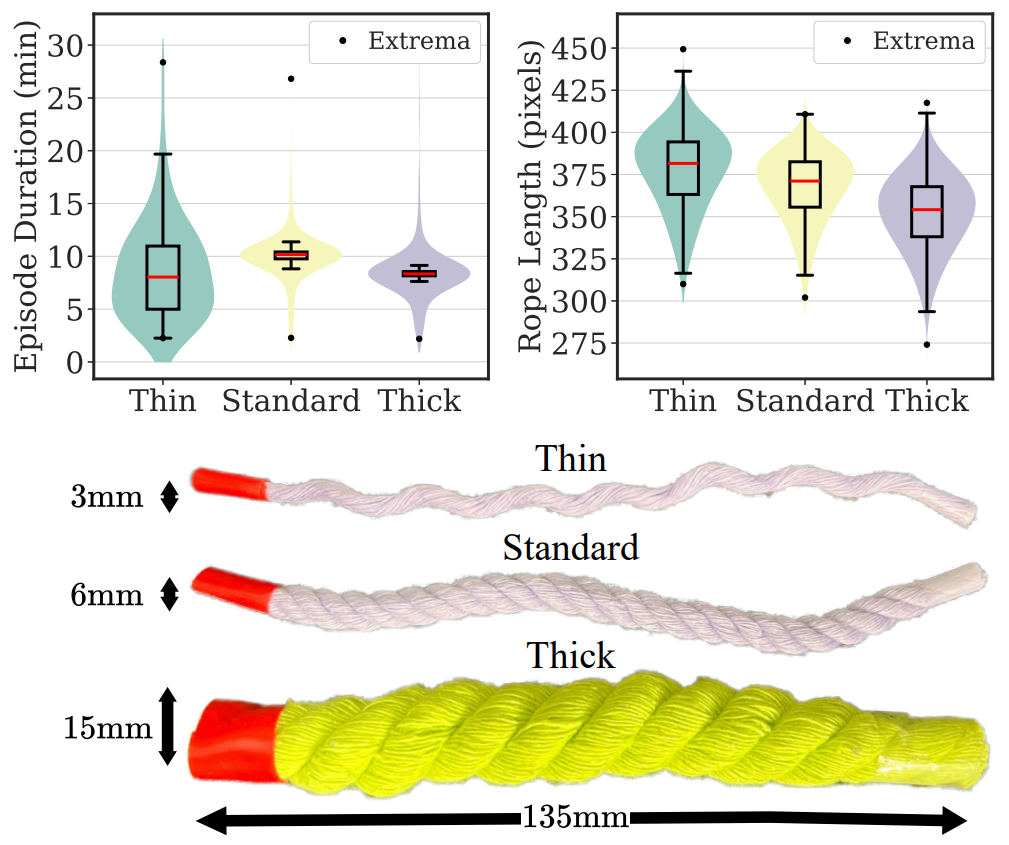
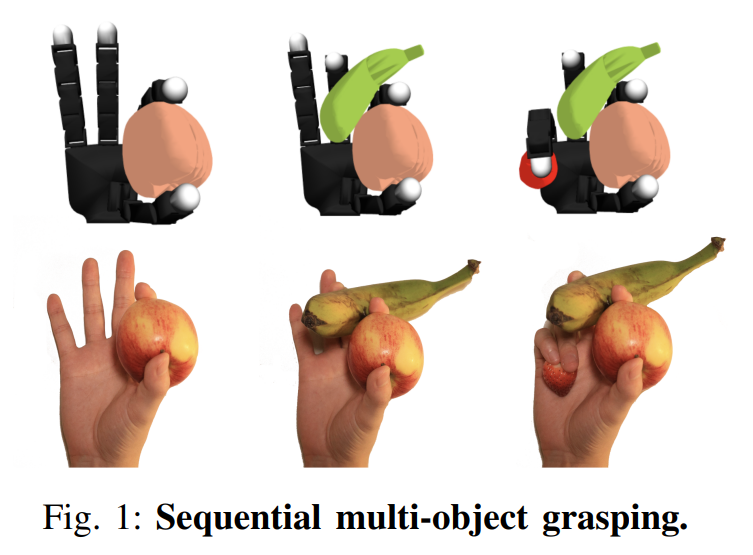
interactions, ranging from studying foundational data-driven robot manipulation primitives to complex interaction scenarios where objects are deformable or fragile.
I currently coordinate two research projects along this research focus. The Horizon Europe project SoftEnable,
and the WASP funded Swedish excellent
research environment (NEST) grant "Intelligent Cloud Robotics for Real-Time
Manipulation at Scale". My group furthermore is funded by additional grants from WASP as well as the Knut and Alice Wallenberg Foundation.
Short Biography
I am currently an Associate Professor of Machine Learning within the division
of Robotics, Perception and Learning at KTH Royal Institute of Technology.
I spent 05/2015-04/2016 at the University of California, Berkeley working in
Prof. Ken Goldberg's group and previously was also a researcher and postdoc
with Prof. Danica Kragic's group at KTH. Before that, I obtained my PhD in mathematics
under supervision of Prof. Michael Singer at the University of Edinburgh.
I hold a BSc mathematics from the University of Edinburgh and a Master of Advanced Study in
Mathematics (Part III) from the University of Cambridge.
Contact
Room 713, Teknikringen 14 RPL, EECS, KTH, 114 28 Stockholm, Sweden, fpokorny (at) kth.se
I am currently looking for master students interested in large scale robotic manipulation and cloud robotics.
If you are interested, please drop me an email with your CV and transcripts attached as well as a reason for why you are
interested in this topic. There are opportunities to work on hardware, machine learning, perception and motion planning. You can also consider the
course DD2411 to work on a project in this direction and get credits. Please note that I only have capacity to consider
students that are already registered at KTH for thesis project work.
This is a personal homepage. Opinions expressed here or implied by links provided do not
represent the official views of KTH Royal Institute of Technology.
© Florian T. Pokorny, all rights reserved.